Đề bài
Mạch điện xoay chiều gồm một điện trở, một cuộn dây và một tụ điện ghép nối tiếp (\(H.15.2).\) Điện áp tức thời giữa hai đầu đoạn mạch \(u = 65\sqrt 2 cos100\pi t(V).\)
Các điện áp hiệu dụng \({U_{AM}} = 13V;{U_{MN}} = 13V;{U_{NB}} = 65V.\)
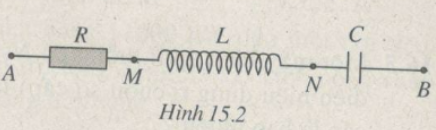
a) Chứng tỏ rằng cuộn dây có điện trở thuần \(r \ne 0.\)
b) Tính hệ số công suất của mạch.
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính điện áp \(U_{AB}^2 = {({U_R} + {U_r})^2} + {({U_L} - {U_C})^2}\)
Sử dụng công thức tính hệ số công suất \(\cos \varphi = \dfrac{{{U_R} + {U_r}}}{{{U_{AB}}}}\)
Lời giải chi tiết
a) Xét \(U_{AM}^2 + {({U_{MN}} - {U_{NB}})^2} \\= {13^2} + {(13 - 65)^2} = 2873\)
\(U_{AB}^2 = {65^2} = 4225\)
Nhận thấy \(U_{AB}^2 \ne {U_{AM}}^2 + {({U_{MN}} - {U_{NB}})^2}\)
Vậy trong cuộn dây còn có điện trở \(r\)
b) Ta có:
\(\begin{array}{l}U_{MN}^2 = U_r^2 + U_L^2\\ \Rightarrow {U_L} = \sqrt {U_{MN}^2 - U_r^2} = \sqrt {{{13}^2} - U_r^2} (1)\end{array}\)
\(\begin{array}{l}U_{AB}^2 = {({U_R} + {U_r})^2} + {({U_L} - {U_C})^2}\\ \Leftrightarrow {65^2} = {(13 + {U_r})^2} + {({U_L} - 65)^2}(2)\end{array}\)
Từ (1)(2)\( \Rightarrow {65^2} = {(13 + {U_r})^2} + {(\sqrt {{{13}^2} - U_r^2} - 65)^2}\)
Giải được \({U_r} = 12V;{U_L} = 5V\)
Hệ số công suất đoạn mạch \(\cos \varphi = \dfrac{{{U_R} + {U_r}}}{{{U_{AB}}}} = \dfrac{{13 + 12}}{{65}} = \dfrac{5}{{13}}\)
soanvan.me
