Đề bài
Cho tam giác ABC vuông tại A, điểm D là trung điểm của BC. Gọi M là điểm đối xứng với D qua AB, E là giao điểm của DM và AB. Gọi N là điểm đối xứng với D qua AC, F là giao điểm của DN và AC.
a. Tứ giác AEDF là hình gì ? Vì sao ?
b. Các tứ giác ADBM, ADCN là hình gì ? Vì sao ?
c. Chứng minh rằng M đối xứng với N qua A
d. Tam giác vuông ABC có điều kiện gì thì tứ giác AEDF là hình vuông ?
Phương pháp giải - Xem chi tiết
Vận dụng kiến thức :
- Tứ giác có ba góc vuông là hình chữ nhật.
- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
- Tính chất về các cạnh và góc của hình thoi; hình vuông.
Lời giải chi tiết
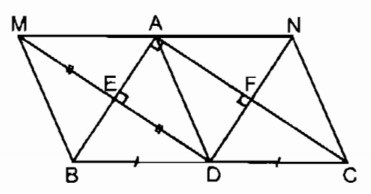
a. Điểm M và điểm D đối xứng qua trục AB
⇒ AB là đường trung trực của đoạn thẳng MD
⇒ AB ⊥ DM
⇒ \(\widehat {AED} = {90^0}\)
Điểm D và điểm N đối xứng nhau qua trục AC ⇒ AC là đường trung trực của đoạn thẳng DN
⇒ AC ⊥ DN \( \Rightarrow \widehat {AFD} = {90^0}\)
Mà \(\widehat {EAF} = {90^0}\) (gt)
Vậy tứ giác AEDF là hình chữ nhật (vì có ba góc vuông)
b. Tứ giác AEDF là hình chữ nhật
⇒ DE // AC; DF // AB
Trong ∆ ABC ta có: DB = DC (gt)
Mà DE // AC
Suy ra: AE = EB (tính chất đường trung bình tam giác)
Lại có DF// AB và DB=DC
Suy ra: AF = FC (tính chất đường trung bình của tam giác)
Xét tứ giác ADBM : AE = EB (chứng minh trên)
ED = EM (vì AB là trung trực của DM)
Suy ra: Tứ giác ADBM là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Mặt khác: AB ⊥ DM
Vậy hình bình hành ADBM là hình thoi ( vì có hai đường chéo vuông góc)
Xét tứ giác ADCN:
AF = FC (chứng minh trên)
DF = FN (vì AC là đường trung trực của DN)
Suy ra: Tứ giác ADCN là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường)
Mà AC ⊥ DN
Vậy hình bình hành ADCN là hình thoi (vì có hai đường chéo vuông góc)
c. Tứ giác ADBM là hình thoi
⇒ AM // DB và AM = AD (tính chất)
Hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi
⇒ AN // DC và AD = AN (tính chất)
Hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng
Và AM = AN nên A là trung điểm của MN
Vậy điểm M và điểm N đối xứng với nhau qua điểm A
d. Hình chữ nhật AEDF trở thành hình vuông khi AE = AF
Ta có: AE = \(\displaystyle {1 \over 2}\)AB ; AF =\(\displaystyle {1 \over 2}\)AC
Nên AE = AF ⇒ AB = AC
Vậy nếu ∆ ABC vuông cân tại A thì tứ giác AEDF là hình vuông.
soanvan.me
