Đề bài
Cho hình chữ nhật có \(O\) là tâm đối xứng. Hỏi có bao nhiêu phép quay tâm \(O\) góc \(\alpha ,0 \le \alpha < 2\pi \), biến hình chữ nhật trên thành chính nó?
A. Không có B. Chỉ có hai
C. Chỉ có ba D. Chỉ có bốn
Phương pháp giải - Xem chi tiết
Vẽ hình và nhận xét.
Lời giải chi tiết
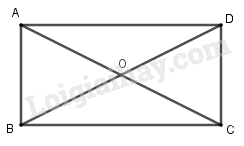
Ta thấy, \({Q_{\left( {O,0} \right)}}\left( A \right) = A,\) \({Q_{\left( {O,0} \right)}}\left( B \right) = B,\) \({Q_{\left( {O,0} \right)}}\left( C \right) = C,\) \({Q_{\left( {O,0} \right)}}\left( D \right) = D\)
Nên \({Q_{\left( {O,0} \right)}}\left( {ABCD} \right) = ABCD\).
\({Q_{\left( {O,\pi } \right)}}\left( A \right) = C,\) \({Q_{\left( {O,\pi } \right)}}\left( B \right) = D,\) \({Q_{\left( {O,\pi } \right)}}\left( C \right) = A,\) \({Q_{\left( {O,\pi } \right)}}\left( D \right) = B\)
Nên \({Q_{\left( {O,0} \right)}}\left( {ABCD} \right) = CDAB\).
Vậy có \(2\) phép quay cần tìm.
Chọn B.
soanvan.me
