Đề bài
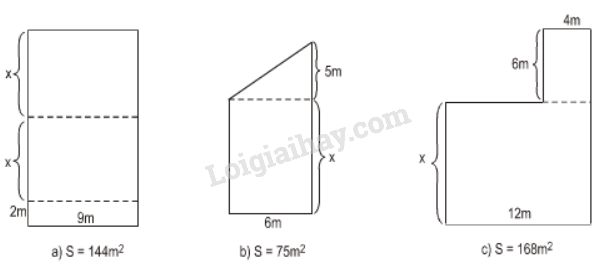
Viết phương trình ẩn x rồi tính x (mét) trong mỗi hình dưới đây (h.4) (S là diện tích của hình):
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Công thức tính diện tích hình chữ nhật: \(S=a\times b\)
Trong đó: \(S\) là diện tích hình chữ nhật
\(a\) là chiều dài hình chữ nhật
\(b\) là chiều rộng hình chữ nhật
Công thức tính diện tích hình thang: \(S = \dfrac{{h\left( {a + b} \right)}}{2}\)
Trong đó: \(S\) là diện tích hình thang
\(a\) và \(b\) là độ dài hai đáy của hình thang
\(h\) là chiều cao của hình thang.
- Để giải các phương trình đưa được về \(ax + b = 0\) ta thường biến đổi phương trình như sau:
+ Quy đồng mẫu hai vế và khử mẫu.
+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng \(ax + b=0\) hoặc \(ax=-b\).
+ Tìm \(x\)
Lời giải chi tiết
a) Chiều dài hình chữ nhật là: \(x+x+2=2x + 2(m)\).
Diện tích hình chữ nhật là \(S = 9(2x + 2)(m^2)\).
Vì diện tích \(S = 144\) m2 nên ta có phương trình:
\(9(2x +2) = 144\)
\(⇔18 x + 18 = 144\)
\(⇔18 x = 144 - 18\)
\(⇔18x = 126\)
\(\Leftrightarrow x=126:18\)
\(⇔ x = 7\)
Vậy \(x = 7\,m\)
b) Đáy nhỏ của hình thang là: \(x(m)\)
Đáy lớn của hình thang là: \(x + 5(m)\)
Diện tích hình thang là: \(S = \dfrac{1}{2}.6.\left( {x + x + 5} \right) = 3.\left( {2x + 5} \right)\) \((m^2)\)
Mà \(S = 75\left( {{m^2}} \right)\) nên ta có phương trình:
\(3(2x + 5) = 75\)
\( \Leftrightarrow 2x + 5 = 75:3\)
\(⇔2x + 5 = 25\)
\( \Leftrightarrow 2x = 25 - 5\)
\(⇔2x = 20\)
\( \Leftrightarrow x = 20:2\)
\(⇔x = 10\)
Vậy \(x = 10\;m\).
c) Biểu thức tính diện tích hình là:
\(S = 12.x + 6.4 = 12x + 24\) \((m^2)\)
Mà \(S = 168\) m2 nên ta có:
\(12x + 24 = 168\)
\( \Leftrightarrow 12x = 168 - 24\)
\( \Leftrightarrow 12x = 144\)
\( \Leftrightarrow x = 144:12\)
\(\Leftrightarrow x = 12\)
Vậy \(x = 12\,m.\)
soanvan.me
