Đề bài
Cho các cặp tia Oa và Ob, Oc và Od là các cặp tia đối nhau. Tìm số đo mỗi góc aOc, bOc, bOd, aOd trong mỗi trường hợp sau:
a) \(\widehat {aOc} = 75^\circ \); b) \(\widehat {aOc} + \widehat {bOd} = 140^\circ \);
c) \(\widehat {aOc} + \widehat {bOd} = \widehat {bOc} + \widehat {aOd}\); d) \(\widehat {bOc} - \widehat {aOc} = 10^\circ \);
e) \(\widehat {bOc} = 2\widehat {aOc}\).
Phương pháp giải - Xem chi tiết
Ta tìm số đo mỗi góc dựa vào những góc đã biết: Hai góc đối đỉnh có số đo góc bằng nhau, hai góc kề bù có tổng số đo góc bằng 180°.
Lời giải chi tiết
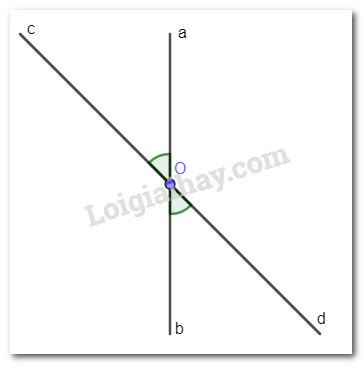
a) \(\widehat {aOc} = \widehat {bOd} = 75^\circ \) (đối đỉnh); \(\widehat {bOc} = \widehat {aOd} = 180^\circ - 75^\circ = 105^\circ \) (hai góc aOc và bOd bù nhau).
b) \(\widehat {aOc} + \widehat {bOd} = 140^\circ \to \widehat {aOc} = \widehat {bOd} = 140^\circ :2 = 70^\circ \); \(\widehat {bOc} = \widehat {aOd} = 180^\circ - 70^\circ = 110^\circ \).
c)
\(\begin{array}{l}\widehat {aOc} + \widehat {bOd} = \widehat {bOc} + \widehat {aOd} \to 2\widehat {aOc} = 2\widehat {bOc}\\ \to \widehat {aOc} = \widehat {bOd} = 180^\circ :2^\circ = 90^\circ \\ \to \widehat {aOc} = \widehat {bOd} = \widehat {bOc} = \widehat {aOd} = 90\end{array}\);
d)
\(\begin{array}{l}\left\{ \begin{array}{l}\widehat {bOc} + \widehat {aOc} = 180^\circ \\\widehat {bOc} - \widehat {aOc} = 10^\circ \end{array} \right.\\ \to \left\{ \begin{array}{l}\widehat {bOc} = \widehat {aOd} = 95^\circ \\\widehat {aOc} = \widehat {bOd} = 85^\circ \end{array} \right.\end{array}\);
e)
\(\begin{array}{l}\left\{ \begin{array}{l}\widehat {bOc} + \widehat {aOc} = 180^\circ \\\widehat {bOc} = 2\widehat {aOc}\end{array} \right.\\ \to 3\widehat {aOc} = 180^\circ \to \widehat {aOc} = \widehat {bOd} = 60^\circ \\ \to \widehat {bOc} = \widehat {aOd} = 120^\circ \end{array}\).
