Đề bài
Quan sát Hình 11. Tính số đo mỗi góc xOy, yOz biết \(\dfrac{1}{5}\widehat {xOz} = \dfrac{1}{4}\widehat {yOz}\).
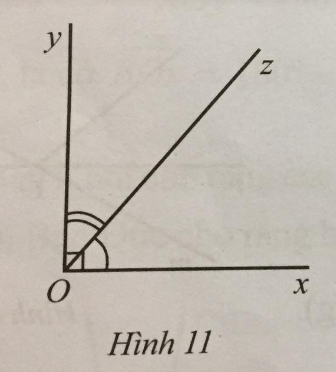
Phương pháp giải - Xem chi tiết
Tìm số đo hai góc dựa vào tỉ số đã cho và tổng hai góc bằng 90°.
Lời giải chi tiết
Ta có: \(\dfrac{1}{5}\widehat {xOz} = \dfrac{1}{4}\widehat {yOz} \to \widehat {xOz} = \dfrac{5}{4}\widehat {yOz}\).
Do hai góc xOz và yOz là hai góc kề nhau nên \(\widehat {xOz} + \widehat {yOz} = \widehat {xOy} = 90^\circ \).
Do đó: \(\dfrac{5}{4}\widehat {yOz} + \widehat {yOz} = 90^\circ \to \dfrac{9}{4}\widehat {yOz} = 90^\circ \to \widehat {yOz} = 90^\circ :\dfrac{9}{4} = 40^\circ \).
Suy ra: \(\widehat {xOz} = 90^\circ - \widehat {yOz} = 90^\circ - 40^\circ = 50^\circ \).
