Đề bài
Chứng minh các định lí:
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Phương pháp giải - Xem chi tiết
a) Chứng minh trung điểm của cạnh huyền cách đều ba đỉnh \(A,B,C.\)
b) Chứng minh : Tâm của đường tròn đó là trung điểm của cạnh huyền.
Lời giải chi tiết
a) (h.62a)
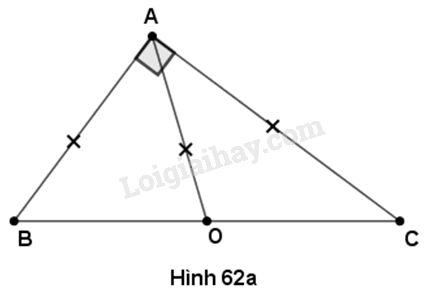
Xét tam giác vuông \(ABC\) vuông tại \(A.\) Gọi \(O\) là trung điểm của \(BC.\) Ta có
\(OA = OB = OC\) vì đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
Suy ra \(O\) là tâm của đường tròn đi qua ba điểm \(A;B;C.\)
Vậy tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) (h. 62b)
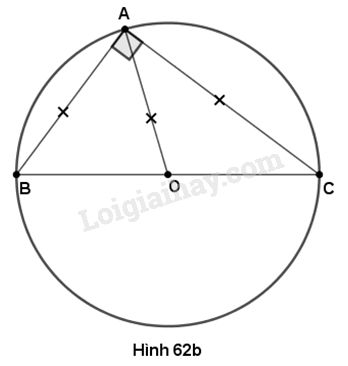
Xét tam giác \(ABC\) nội tiếp đường tròn \((O)\) đường kính \(BC,\) ta có \(OA = OB = OC.\)
Tam giác \(ABC\) có đường trung tuyến \(AO\) bằng \(\dfrac{1}{2}BC\) nên \(\widehat {BAC} = {90^o}.\)
Vậy tam giác \(ABC\) vuông tại \(A.\)
soanvan.me
