Đề bài
Cho góc nhọn \(xAy\) và hai điểm \(B, C\) thuộc tia \(Ax.\) Dựng đường tròn \((O)\) đi qua \(B\) và \(C\) sao cho tâm \(O\) nằm trên tia \(Ay.\)
Phương pháp giải - Xem chi tiết
- Xác định tâm và bán kính
- Tâm \(O\) phải thỏa mãn hai điều kiện, trong đó có một điều kiện là nằm trên đường trung trực của \(BC.\)
Lời giải chi tiết
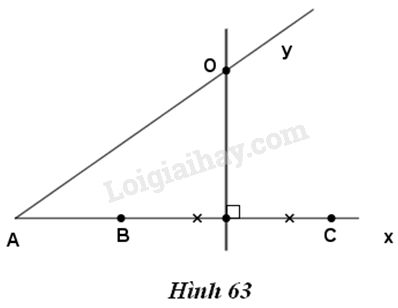
a) Cách dựng
- Dựng đường trung trực của \(BC,\) cắt \(Ay\) ở \(O.\)
- Dựng đường tròn tâm \(O\) bán kính \(OB.\)
b) Chứng minh
\(O\) thuộc đường trung trực của \(BC\) nên \(OB = OC.\)
Đường tròn \(\left( {O;OB} \right)\) có \(O \in Oy,\) đi qua \(B,C\).
soanvan.me
