Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:
LG a
3x – y =2
Phương pháp giải:
Tập nghiệm của phương trình \({\rm{ax}} + by = c\) biểu diễn bởi đường thẳng \(d:{\rm{ }}ax + by = c.\)
+) Nếu a≠0 và b=0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x = \dfrac{c}{a}\\y \in R\end{array} \right.\) và đường thẳng d song song hoặc trùng với trục tung.
+) Nếu a=0 và b≠0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x \in R\\y = \dfrac{c}{b}\end{array} \right.\) và đường thẳng d song song hoặc trùng với trục hoành.
+) Nếu a≠0 và b≠0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x \in R\\y = - \dfrac{a}{b}x + \dfrac{c}{b}\end{array} \right.\) và đường thẳng d là đồ thị hàm số \(y = - \dfrac{a}{b}x + \dfrac{c}{b}\)
Lời giải chi tiết:
Ta có \(3x - y = 2 \Leftrightarrow y = 3x - 2\)
Vậy nghiệm tổng quát của phương trình là \(\left( {x;3x - 2} \right)\) với \(x \in \mathbb{R}\) .
Đường thẳng biểu diễn tập nghiệm của nó đi qua hai điểm \(A\left( {0; - 2} \right)\) và \(B\left( {2;4} \right)\).
Vẽ hình 2:

LG b
x + 5y = 3
Phương pháp giải:
Tập nghiệm của phương trình \({\rm{ax}} + by = c\) biểu diễn bởi đường thẳng \(d:{\rm{ }}ax + by = c.\)
+) Nếu a≠0 và b=0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x = \dfrac{c}{a}\\y \in R\end{array} \right.\) và đường thẳng d song song hoặc trùng với trục tung.
+) Nếu a=0 và b≠0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x \in R\\y = \dfrac{c}{b}\end{array} \right.\) và đường thẳng d song song hoặc trùng với trục hoành.
+) Nếu a≠0 và b≠0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x \in R\\y = - \dfrac{a}{b}x + \dfrac{c}{b}\end{array} \right.\) và đường thẳng d là đồ thị hàm số \(y = - \dfrac{a}{b}x + \dfrac{c}{b}\)
Lời giải chi tiết:
Ta có \(x + 5y = 3 \Leftrightarrow x = 3 - 5y\)
Vậy nghiệm tổng quát của phương trình là \(\left( {3 - 5y;y} \right)\) với \(y \in \mathbb{R}\) .
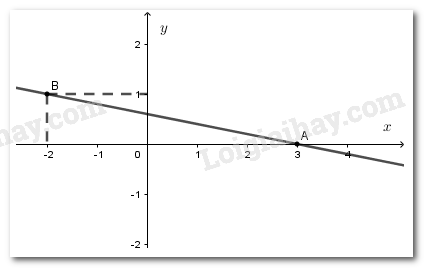
Đường thẳng biểu diễn tập nghiệm của nó đi qua hai điểm \(A\left( {3;0} \right)\) và \(B\left( { - 2;1} \right)\).
Vẽ hình 3:
LG c
4x – 3y = -1
Phương pháp giải:
Tập nghiệm của phương trình \({\rm{ax}} + by = c\) biểu diễn bởi đường thẳng \(d:{\rm{ }}ax + by = c.\)
+) Nếu a≠0 và b=0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x = \dfrac{c}{a}\\y \in R\end{array} \right.\) và đường thẳng d song song hoặc trùng với trục tung.
+) Nếu a=0 và b≠0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x \in R\\y = \dfrac{c}{b}\end{array} \right.\) và đường thẳng d song song hoặc trùng với trục hoành.
+) Nếu a≠0 và b≠0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x \in R\\y = - \dfrac{a}{b}x + \dfrac{c}{b}\end{array} \right.\) và đường thẳng d là đồ thị hàm số \(y = - \dfrac{a}{b}x + \dfrac{c}{b}\)
Lời giải chi tiết:
Ta có \(4x - 3y = - 1 \Leftrightarrow y = \dfrac{4}{3}x + \dfrac{1}{3}\)
Vậy nghiệm tổng quát của phương trình là \(\left( {x;\dfrac{4}{3}x + \dfrac{1}{3}} \right)\) với \(x \in \mathbb{R}\) .
Đường thẳng biểu diễn tập nghiệm của nó đi qua hai điểm \(A\left( { - 1; - 1} \right)\) và \(B\left( {2;3} \right)\).
Vẽ hình 4:

LG d
0x + 2y = 5
Phương pháp giải:
Tập nghiệm của phương trình \({\rm{ax}} + by = c\) biểu diễn bởi đường thẳng \(d:{\rm{ }}ax + by = c.\)
+) Nếu a≠0 và b=0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x = \dfrac{c}{a}\\y \in R\end{array} \right.\) và đường thẳng d song song hoặc trùng với trục tung.
+) Nếu a=0 và b≠0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x \in R\\y = \dfrac{c}{b}\end{array} \right.\) và đường thẳng d song song hoặc trùng với trục hoành.
+) Nếu a≠0 và b≠0 thì phương trình có nghiệm \(\left\{ \begin{array}{l}x \in R\\y = - \dfrac{a}{b}x + \dfrac{c}{b}\end{array} \right.\) và đường thẳng d là đồ thị hàm số \(y = - \dfrac{a}{b}x + \dfrac{c}{b}\)
Lời giải chi tiết:
Ta có \(0x + 2y = 5 \Leftrightarrow y = \dfrac{5}{2}\)
Vậy nghiệm tổng quát của phương trình là \(\left( {x;\dfrac{5}{2}} \right)\) với \(x \in \mathbb{R}\) .
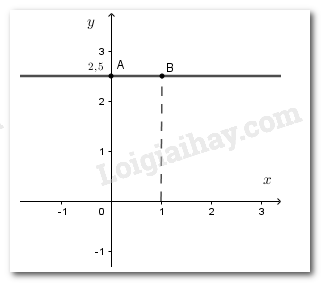
Đường thẳng biểu diễn tập nghiệm của nó đi qua hai điểm \(A\left( {0;\dfrac{5}{2}} \right)\) và \(B\left( {1;\dfrac{5}{2}} \right)\).
Vẽ hình 5:
soanvan.me
