Đề bài
Cho hai phương trình \(x + 2y = 4\) và \(x – y = 1.\) Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ trục tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của những phương trình nào ?
Phương pháp giải - Xem chi tiết
Tập nghiệm của phương trình \({\rm{ax}} + by = c\) biểu diễn bởi đường thẳng \(d:{\rm{ }}ax + by = c.\)
Có thể vẽ đường thẳng \(d:{\rm{ }}ax + by = c\) bằng cách vẽ đường thẳng đi qua hai điểm \(\left( {0;\dfrac{c}{b}} \right)\) và \(\left( {\dfrac{c}{a};0} \right)\) với \(a \ne 0.\)
Vẽ các đường thẳng biểu diễn tập nghiệm của các phương trình đã cho. Sau đó xác định tọa độ giao điểm của hai đường thẳng.
Lời giải chi tiết
Tập nghiệm của phương trình \(x + 2y = 4\) được biểu diễn bởi đường thẳng \(\left( {{d_1}} \right)\) đi qua hai điểm \(\left( {0;2} \right)\) và \(\left( {4;0} \right)\)
Tập nghiệm của phương trình \(x - y = 1\) được biểu diễn bởi đường thẳng \(\left( {{d_2}} \right)\) đi qua hai điểm \(\left( {0; - 1} \right)\) và \(\left( {1;0} \right)\)
Vẽ hình 6:
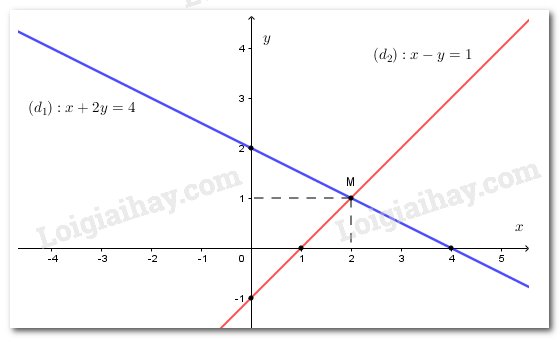
Trên hình 6 ta thấy \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) cắt nhau tại \(M\left( {2;1} \right)\)
Tọa độ của điểm \(M\left( {2;1} \right)\) thỏa mãn phương trình \(x + 2y = 4\) vì khi thay \(x = 2\) và \(y = 1\) vào vế trái, ta có \(2 + 2.1 = 4.\)
Tọa độ của điểm \(M\left( {2;1} \right)\) thỏa mãn phương trình \(x - y = 1\) vì khi thay \(x = 2\) và \(y = 1\) vào vế trái, ta có \(2 - 1 = 1.\)
Chú ý:
Sai lầm dễ mắc phải là học sinh vẽ các đường thẳng không chính xác, dẫn đến xác định sai tọa độ giao điểm \(M.\)
soanvan.me
