Bài 22 trang 127 Vở bài tập toán 9 tập 1

Đề bài

Cho đường tròn \((O)\), điểm \(A\) nằm bên ngoài đường tròn. Kẻ các tiếp tuyến \(AB,\ AC\) với đường tròn (\(B,\ C\) là các tiếp điểm).

a) Chứng minh rằng \(OA\) vuông góc với \(BC\).

b) Vẽ đường kính \(CD\). Chứng minh rằng \(BD\) song song với \(AO\).

c) Tính độ dài các cạnh của tam giác \(ABC\); biết \(OB=2cm,\ OA=4cm\).

Lời giải chi tiết

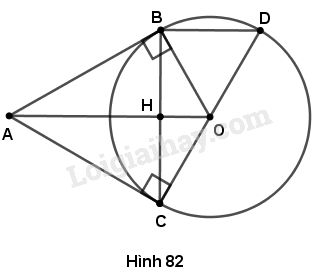
a) Theo tính chất hai tiếp tuyến cắt nhau tại \(A\) ta có :

\(AB = AC,\widehat {OAB} = \widehat {OAC}.\)

Tam giác \(ABC\) có hai cạnh bằng nhau nên là tam giác cân, lại có \(AO\) là tia phân giác nên \(AO \bot BC.\)

b) Ta chứng minh \(OH\) là đường trung bình của tam giác \(CBD.\) Gọi \(H\) là giao điểm của và \(BC.\) Ta có

\(BH = HC\) (vì trong tam giác cân tia phân giác hạ từ đỉnh đồng thời là đường trung tuyến).

Mặt khác, \(DO = CO\) (bán kính) nên \(OH\) là đường trung bình của tam giác \(CBD,\) suy ra \(BD//OH,\) tức là \(BD//AO.\)

c) Tính \(AC:\) Áp dụng định lí Py-ta-go ta có : \(A{C^2} = A{B^2} = A{O^2} - B{O^2}\)\( = {4^2} - {2^2} = 12\left( {cm} \right)\)

suy ra \(AC = \sqrt {12}  = 2\sqrt 3 \left( {cm} \right).\)

Xét tam giác vuông \(OAC,\) ta có \(\sin \widehat {OAC} = \dfrac{{OC}}{{OA}} = \dfrac{2}{4} = \dfrac{1}{2}\) nên \(\widehat {AOC} = {30^o},\) do đó \(\widehat {BAC} = 2.\widehat {OAC} = {60^o}.\)

Tam giác \(ABC\) là tam giác đều vì là tam giác cân có một góc \({60^o}\). 

Do đó \(AB = BC = AC = 2\sqrt 3 \left( {cm} \right).\)

Chú ý :

Câu b) còn có thể giải theo cách khác như sau :

Chứng minh \(BD \bot BC\) và \(AO \bot BC\) từ đó suy ra \(BD//AO.\)

soanvan.me