Đề bài
Cho ba mặt phẳng \(\left( \alpha \right),\left( \beta \right),\left( \gamma \right)\) song song với nhau. Hai đường thẳng \(a\) và \(a’\) cắt ba mặt phẳng ấy theo thứ tự nói trên tại \(A\), \(B\), \(C\) và \(A’\), \(B’\), \(C’\). Cho \(AB = 5,BC = 4,A'C' = 18\). Tính độ dài \(A’B’\), \(B’C’\).
Phương pháp giải - Xem chi tiết
Sử dụng định lý Talet.
Lời giải chi tiết
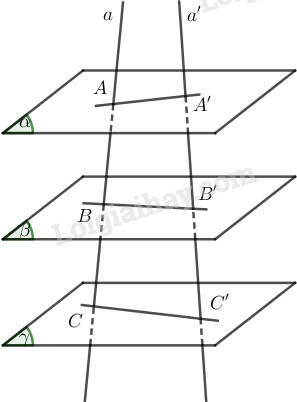
Vì \((\alpha)\parallel (\beta)\parallel (\gamma)\) nên \(\dfrac{AB}{A’B’}=\dfrac{BC}{B’C’}\).
Mà \(\dfrac{AB}{A’B’}=\dfrac{BC}{B’C’}\)
\(=\dfrac{AB+BC}{A’B’+B’C’}=\dfrac{AC}{A’C’}\).
Suy ra : \(A’B’=\dfrac{A’C’.AB}{AC}=\dfrac{18.5}{9}=10\).
\(B’C’=\dfrac{A’C’.BC}{AC}=\dfrac{18.4}{9}=8\).
soanvan.me
