Cho hai tia \(Ax\), \(By\) chéo nhau. Lấy \(M\), \(N\) lần lượt là các điểm di động trên \(Ax\), \(By\). Gọi \(\left( \alpha \right)\) là mặt phẳng chứa \(By\) và song song với \(Ax\). Đường thẳng qua \(M\) và song song với \(AB\) cắt \(\left( \alpha \right)\) tại \(M’\).
LG a
Tìm tập hợp điểm \(M’\).
Phương pháp giải:
Sử dụng tính chất: Nếu mặt phẳng \((\alpha)\) và \((\beta)\) có điểm chung \(S\) và lần lượt chứa hai đường thẳng song song \(d\) và \(d'\) thì giao tuyến của \((\alpha)\) và \((\beta)\) là đường thẳng \(\Delta\) đi qua \(S\) và song song với \(d\) và \(d'\).
Sử dụng tính chất: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung (giao tuyến) đi qua điểm chung ấy.
Lời giải chi tiết:
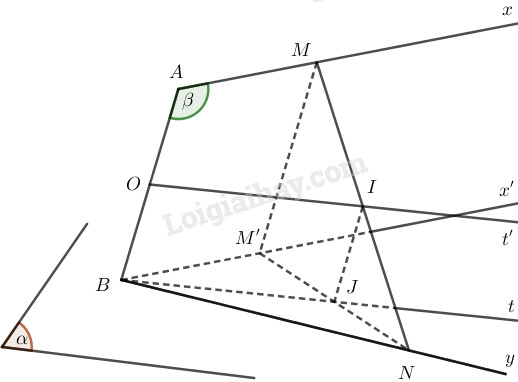
Gọi \((\beta)\) là mặt phẳng xác định bởi hai đường thẳng \(AB\) và \(Ax\).
Do \(Ax\parallel (\alpha)\) nên \((\beta)\cap (\alpha)=Bx', Bx'\parallel Ax\) .
Ta có \(M'\) là điểm chung của \((\alpha)\) và \((\beta)\) nên \(M'\in Bx'\).
Khi \(M\) trùng với \(A\) thì \(M'\) trùng \(B\) nên tập hợp \(M'\) là tia \(Bx'\).
LG b
Gọi \(I\) là trung điểm của \(MN\). Tìm tập hợp các điểm \(I\) khi \(AM = BN\)
Phương pháp giải:
Sử dụng tính chất của hình bình hành.
Sử dụng phép tịnh tiến.
Lời giải chi tiết:
Ta có tứ giác \(ABM'M\) là hình bình hành nên \(BM'=AM=BN\).
Tam giác \(BM'N\) cân tại \(B\)
Suy ra trung điểm \(J\) của cạnh đáy \(NM'\) thuộc phân giác trong \(Bt\) của góc \(B\) trong tam giác \(BNM'\). Ta có \(Bt\) cố định.
Gọi \(O\) là trung điểm của \(AB\). Trong mặt phẳng \((AB,Bt)\), tứ giác \(OBIJ\) là hình bình hành nên \(\vec {JI}=\vec{BO}\).
Do đó \(I\) là ảnh của \(J\) trong phép tịnh tiến theo vectơ \(\vec{BO}\).
Vậy tập hợp \(I\) là tia \(Ot'\), \(Ot'\parallel Bt\).
soanvan.me
