Đề bài
Cho hàm số y = -2x + 3
a) Vẽ đồ thị của hàm số
b) Tính góc tạo bởi đường thẳng y = -2x + 3 và trục Ox (làm tròn đến phút).
Phương pháp giải - Xem chi tiết
a) Cách vẽ đồ thị hàm số y = ax + b (trường hợp \(a \ne 0\) và \(b \ne 0\))
- Cho x = 0 thì y = b, được điểm P(0 ; b) thuộc trục tung Oy.
- Cho y = 0 thì \(x = - \dfrac{b}{a}\), được điểm \(Q\left( { - \dfrac{b}{a};0} \right)\) thuộc trục hoành Ox.
- Vẽ đường thẳng đi qua hai điểm P và Q
b) Số a được gọi là hệ số góc của đường thẳng y = ax + b.
- Khi a > 0, ta có \(\tan \alpha = a\)
- Khi a < 0, ta có \(\tan \left( {{{180}^o} - \alpha } \right) = \left| a \right|\)
Lời giải chi tiết
a)
- Cho \(x = 0\) thì \(y = 3\), được điểm \(C\left( {0;3} \right)\)
- Cho \(y = 0\) thì \(x = \dfrac{3}{2}\) , được điểm \(D\left( {\dfrac{3}{2};0} \right)\)
- Vẽ đường thẳng đi qua hai điểm C và D ta được đồ thị của hàm số đã cho.
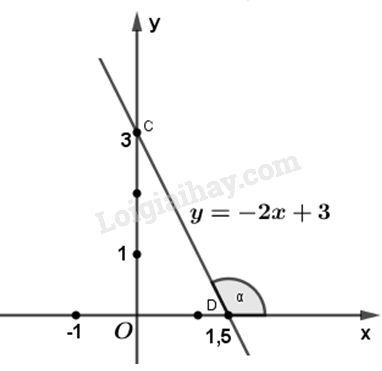
b) Gọi \(\alpha \) là góc tạo bởi đường thẳng y = -2x + 3 và trục Ox
Ta có \(\tan \left( {{{180}^o} - \alpha } \right) = \left| { - 2} \right| = 2\)
Tính trên máy được :
\({180^o} - \alpha \approx {63^o}26'\) \( \Rightarrow \alpha \approx {180^o} - {63^o}26' = {116^o}34'\)
soanvan.me
