Đề bài
Hình thang \(ABCD\) có đáy \(AB, CD.\) Gọi \(E, F, K\) theo thứ tự là trung điểm của \(AD, BC, BD.\) Chứng minh ba điểm \(E, K, F\) thẳng hàng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng:
- Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Tiên đề Ơclit: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Lời giải chi tiết
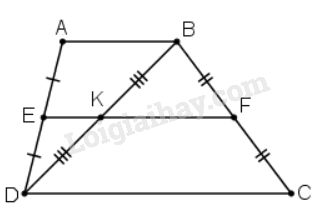
- Xét \(\Delta AB{\rm{D}}\) có: \(E, K\) lần lượt là trung điểm của \(AD, BD\) (giả thiết)
\( \Rightarrow EK\) là đường trung bình của \(\Delta AB{\rm{D}}\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow EK // AB\) (tính chất đường trung bình của tam giác) (1)
- Xét \(\Delta DB{\rm{C}}\) có: \(F, K\) lần lượt là trung điểm của \( BC, BD\) (giả thiết)
\( \Rightarrow FK\) là đường trung bình của \(\Delta DB{\rm{C}}\) (dấu hiệu nhận biết đường trung bình của tam giác)
\( \Rightarrow FK // DC\) (tính chất đường trung bình của tam giác)
Mặt khác, \(AB // DC\) (vì \(ABCD\) là hình thang) nên suy ra \(FK // AB\) (2)
Từ (1) và (2) ta có qua điểm \(K\) không thuộc \(AB\) có hai đường thẳng \(EK\) và \(FK\) cùng \(//AB\) nên theo tiên đề Ơ-clit thì ba điểm \(E, K, F\) thẳng hàng .
soanvan.me
