Đề bài
Cho \(AB\) và \(CD\) là hai đường kính vuông góc của đường tròn \((O)\). Trên cung nhỏ \(BD\) lấy một điểm \(M\). Tiếp tuyến tại \(M\) cắt tia \(AB\) ở \(E\), đoạn thẳng \(CM\) cắt \(AB\) ở \(S\). Chứng minh \(SE = EM\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức :
+ Số đo của góc đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn
Từ đó chứng minh \(\Delta ESM\) cân tại \(E\) để suy ra hai cạnh bên bằng nhau.
Lời giải chi tiết
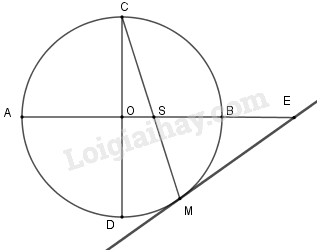

Vì \(AB \bot CD\) tại \(O\) nên ta có \(\overparen{AC}=\overparen{CB}\) \(=\overparen{AD} = \overparen{BD}\)
- Góc \(CSA\) là góc có đỉnh bên trong đường tròn
Do đó, \(\widehat {CSA} = \dfrac{1}{2}\)(sđ \(\overparen{AC}+\) sđ\(\overparen{BM}\)) (1)
- Góc \(CME\) là góc tạo bởi tia tiếp tuyến và dây cung
Do đó, \(\widehat {CME} = \dfrac{1}{2}\) sđ\(\overparen{CM} = \dfrac{1}{2}\)(sđ \(\overparen{CB}+\) sđ\(\overparen{BM}\)) (2)
Theo giả thiết \(\overparen{AC}=\overparen{CB}\) \(=\overparen{AD} = \overparen{BD}\)
Từ (1) và (2) suy ra \(\widehat {CSA} = \widehat {CME}\)
Mà \(\widehat{CSA} = \widehat{ESM}\) vì hai góc đối đỉnh \(\Rightarrow \widehat{ESM}= \widehat {CME}\)
Vậy \(\Delta MES\) là tam giác cân tại \(E\) nên \(ES = EM.\)
soanvan.me
