Đề bài
Qua điểm \(A\) nằm bên ngoài đường tròn \((O)\) vẽ hai cát tuyến \(ABC\) và \(AMN\) sao cho hai đường thẳng \(BN\) và \(CM\) cắt nhau tại \(S\) nằm bên trong đường tròn. Chứng minh
\(\widehat A + \widehat {BSM} = 2.\widehat {CMN}\) .
Phương pháp giải - Xem chi tiết
Sử dụng:
+ Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
+ Số đo của góc đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo góc nội tiếp bằng nửa số đo cung bị chắn.
Lời giải chi tiết
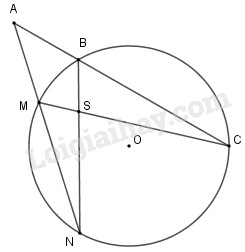

Theo giả thiết \(\widehat A = \dfrac{1}{2}\) (sđ \(\overparen{NC}-\) sđ\(\overparen{BM}\)) (1)
\(\widehat {BSM} = \dfrac{1}{2}\)(sđ\(\overparen{NC}+\) sđ\(\overparen{BM}\)) (2)
Ta có \(\widehat {CMN} = \dfrac{1}{2}\) sđ \(\overparen{NC}\) vì góc nội tiếp chắn cung \(NC.\) (3)
Vậy từ (1), (2), (3) ta có \(\widehat A + \widehat {BSM} = 2\widehat {CMN}\).
soanvan.me
