Đề bài
Chỉ có 1 cái ô xanh, 1 cái ô trắng, 1 cái mũ xanh, 1 cái mũ trắng, 1 cái mũ đen, 1 đôi giày đen, 1 đôi giày trắng. Chi chọn ngẫu nhiên 1 cái ô, 1 cái mũ và 1 đôi giày để đến trường
a) Hãy vẽ sơ đồ mô tả các kết quả có thể xảy ra
b) Tính xác suất của biến cố “Chỉ có 1 trong 3 thứ đồ Chi chọn có màu trắng”
Phương pháp giải - Xem chi tiết
Phép thử có không gian mẫu gồm hữu hạn các kết quả có cùng khả năng xảy ra và A là 1 biến cố
Xác suất của biến cố A là một số, kí hiệu \(P\left( A \right)\) được xác định bởi công thức: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}}\), trong đó \(n\left( A \right)\) và \(n\left( \Omega \right)\) lần lượt là kí hiệu số phần tử của tập A và \(\Omega \)
Lời giải chi tiết
a)
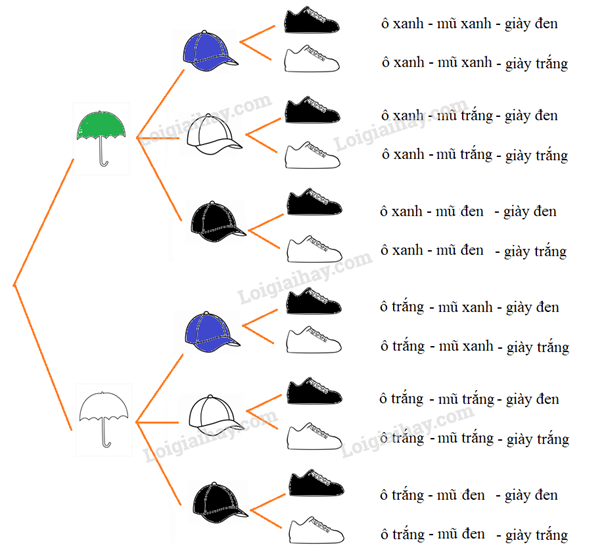
b)
Dựa vào sơ đồ cây, ta có số cách chọn 1 ô, 1 mũ và 1 đôi giày là 12 cách.
Do đó \(n\left( \Omega \right) = 2.3.2 = 12\)
Gọi A là biến cố “Chỉ có 1 trong 3 thứ đồ Chi chọn có màu trắng”
Nhìn vào sơ đồ cây, Chi có các cách chọn là:
Ô trắng -mũ xanh – giày đen
Ô trắng -mũ đen – giày đen
Ô xanh -mũ xanh – giày trắng
Ô xanh -mũ trắng – giày đen
Ô xanh -mũ đen – giày trắng
\( \Rightarrow n\left( A \right) = 5\)
\( \Rightarrow P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{5}{{12}}\)
