Đề bài
Cho tam giác ABC vuông tại A có \(\dfrac{{AB}}{{AC}} = \dfrac{3}{4}\), đường cao AH = 18 cm. Tính chu vi tam giác ABC.
Phương pháp giải - Xem chi tiết
Áp dụng hệ thức lượng trong tam giác vuông để tìm mối quan hệ nữa giữa AB và AC, từ đó sử dụng phương pháp rút thế để tinh.
Lời giải chi tiết
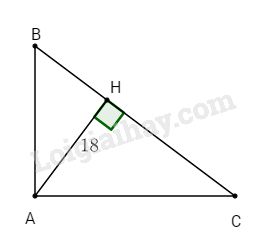
Có \(\dfrac{{AB}}{{AC}} = \dfrac{3}{4} \Rightarrow AB = \dfrac{3}{4}AC\)
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A, đường cao AH:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \\\Leftrightarrow \dfrac{1}{{{{18}^2}}} = \dfrac{{16}}{{9A{C^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{{25}}{{9A{C^2}}} \\\Leftrightarrow A{C^2} = \dfrac{{{{25.18}^2}}}{9}\)
\( \Rightarrow AC = \dfrac{{5.18}}{3} = 30\,\)(cm) \( \Rightarrow AB = \dfrac{3}{4}AC = \dfrac{3}{4}.30 = \dfrac{{45}}{2}\)(cm)
\(AB.AC = AH.BC\\ \Rightarrow BC = \dfrac{{AB.AC}}{{AH}} = \dfrac{{45.30}}{{2.18}} = \dfrac{{75}}{2}\)(cm)
Chu vi tam giác ABC là: \({C_{\Delta ABC}} = AB + AC + BC \)\(\,= \dfrac{{45}}{2} + 30 + \dfrac{{75}}{2} = 90\) (cm)
soanvan.me
