Đề bài
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại điểm A. Hai dây cung BA và CA của (O) kéo dài cắt (O’) lần lượt tại D và E. Chứng minh \(\widehat {ABC} = \widehat {ADE}\).
Phương pháp giải - Xem chi tiết
+) Dựng tiếp tuyến chung của hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tại A.
+) Sử dụng tính chất: Trong một đường tròn, góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn 1 cung thì bằng nhau.
Lời giải chi tiết
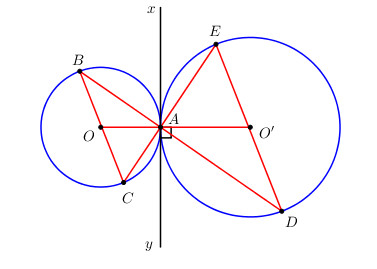
Qua A kẻ đường thẳng \(xy \bot OO'\), khi đó xy là tiếp tuyến chung của 2 đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tại A.
Xét đường tròn \(\left( O \right)\) ta có: \(\widehat {ABC} = \widehat {CAy}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cing cùng chắn cung AC).
Xét đường tròn \(\left( {O'} \right)\) ta có: \(\widehat {ADE} = \widehat {EAx}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cing cùng chắn cung AE).
Mà \(\widehat {CAy} = \widehat {EAx}\) (hai góc đối đỉnh).
Vậy \(\widehat {ABC} = \widehat {ADE}\) (đpcm).
soanvan.me
