Đề bài
Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Qua M vẽ tiếp tuyến tiếp xúc với (O) tại A và vẽ cát tuyến MBC đi qua O (B nằm giữa M và C). Đường tròn đường kính MB cắt MA tại E. Chứng minh số đo cung nhỏ AC bằng tổng số đo hai cung nhỏ BA và BE.
Phương pháp giải - Xem chi tiết
+) Đưa mối quan hệ về góc cần chứng minh về mối quan hệ giữa các số đo cung.
+) Sử dụng tính chất: Góc nội tiếp bằng nửa số đo cung bị chắn, góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn.
Lời giải chi tiết
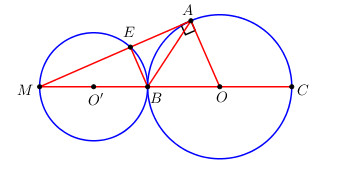
Xét tam giác ABM có: \(\widehat {ABC} = \widehat {AMB} + \widehat {BAM}\) (Góc ngoài của 1 tam giác bằng tổng hai góc trong không kề với nó).
Xét đường tròn \(\left( O \right)\) có: \(\widehat {ABC} = \dfrac{1}{2}sd\,cungAC\) (góc nội tiếp bằng nửa số đo cung bị chắn)
\(\widehat {BAM} = \dfrac{1}{2}sd\,cung\,AB\) (góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo cung bị chắn)
Xét đường tròn \(\left( {O'} \right)\) có: \(\widehat {AMB} = \dfrac{1}{2}sd\,cung\,BE\) (góc nội tiếp bằng nửa số đo cung bị chắn AE).
Vậy \(sd\,cungAC\)\(=sd\,cungAB\)\(+sd\,cungBE\)
soanvan.me
