Đề bài
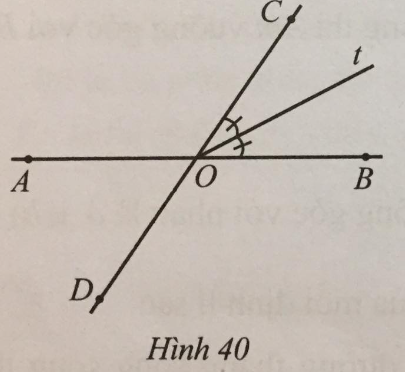
Ở Hình 40 có AB và CD cắt nhau tại O, Ot là tia phân giác của góc BOC, \(\widehat {AOC} - \widehat {BOC} = 68^\circ \). Số đo góc BOt là:
A. 56°. B. 62°. C. 28°. D. 23°.
Phương pháp giải - Xem chi tiết
+ Hai góc AOC và BOC là hai góc kề bù nhau. Sử dụng tính chất tổng 2 góc kề bù là 180 độ.
+ Tính chất tia phân giác của một góc.
Lời giải chi tiết
Ta có: \(\widehat {BOC} = \widehat {AOD}\) (đối đỉnh).
Suy ra: \(\widehat {AOC} - \widehat {BOC} = \widehat {AOC} - \widehat {AOD} = 68^\circ \) mà \(\widehat {AOC} + \widehat {AOD} = 180^\circ \).
Suy ra: \(\left\{ \begin{array}{l}\widehat {AOC} = 124^\circ \\\widehat {AOD} = \widehat {BOC} = 56^\circ \end{array} \right.\).
Mà Ot là tia phân giác của góc BOC nên \(\widehat {BOt} = \dfrac{1}{2}\widehat {BOC} = \dfrac{{56^\circ }}{2} = 28^\circ \).
Đáp án: C. 28°.
