Đề bài
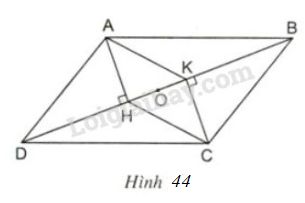
Cho hình \(44\), trong đó \(ABCD\) là hình bình hành.
a) Chứng minh rằng \(AHCK\) là hình bình hành.
b) Gọi \(O\) là trung điểm của \(HK\). Chứng minh rằng ba điểm \(A, O, C\) thẳng hàng
Phương pháp giải - Xem chi tiết
Sử dụng:
+) Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+) Tính chất hình bình hành: Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Lời giải chi tiết
a) Các tam giác vuông \(AHD\) và \(CKB\) có:
\( AD = CB\) (cạnh đối của hình bình hành)
\(\widehat {ADH} = \widehat {CBK}\) (so le trong, \(AD//BC\))
Do đó \(∆AHD = ∆CKB\) (cạnh huyền - góc nhọn), suy ra \(AH = CK\)
Tứ giác \(AHCK\) có \(AH//CK\) (cùng vuông góc với \(BD\)), \(AH = CK\) (chứng minh trên) nên \(AHCK\) là hình bình hành.
b) Xét hình bình hành \(AHCK\). Theo tính chất đường chéo hình bình hành, trung điểm \(O\) của đường chéo \(HK\) cũng là trung điểm của đường chéo \(AC.\)
Do đó ba điểm \(A,O,C\) thẳng hàng.
Lưu ý: Trong hình bình hành, trung điểm của một đường chéo và hai đầu mút của đường chéo kia là ba điểm thẳng hàng.
soanvan.me
