Đề bài
Tam giác \(ABC\) có ba đường trung tuyến cắt nhau tại \(O.\) Gọi \(P, Q, R\) thứ tự là trung điểm của các đoạn thẳng \(OA, OB, OC.\)
Chứng minh rằng tam giác \(PQR\) đồng dạng với tam giác \(ABC.\)
Phương pháp giải - Xem chi tiết
Sử dụng:
- Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
- Tính chất: Đường trung bình tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
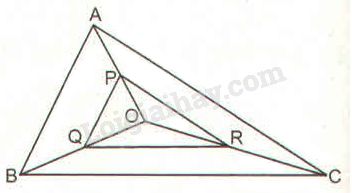
Xét \( ∆ OAB\) có \(PQ\) là đường trung bình nên \(\displaystyle PQ = {1 \over 2}AB\) (tính chất đường trung bình của tam giác).
\( \Rightarrow \displaystyle {{PQ} \over {AB}} = {1 \over 2}\) (1)
Xét \(∆ OAC\) có \(PR\) là đường trung bình nên \(\displaystyle PR = {1 \over 2}AC\) (tính chất đường trung bình của tam giác)
\( \Rightarrow \displaystyle {{PR} \over {AC}} = {1 \over 2}\) (2)
Xét \(∆ OBC\) có \(QR\) là đường trung bình nên \(\displaystyle QR = {1 \over 2}BC\) (tính chất đường trung bình của tam giác )
\( \Rightarrow \displaystyle{{QR} \over {BC}} = {1 \over 2}\) (3)
Từ (1), (2) và (3) suy ra: \(\displaystyle {{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}}= {1 \over 2}\)
Vậy \(∆ PQR\) đồng dạng \(∆ ABC\) (c.c.c).
soanvan.me
