Đề bài
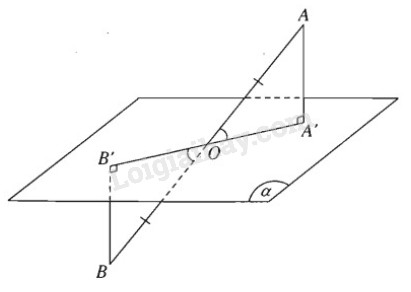
Một đoạn thẳng \(AB\) không vuông góc với mặt phẳng \(\left( \alpha \right)\) cắt mặt phẳng này tại trung điểm \(O\) của đoạn thẳng đó. Các đường thẳng vuông góc với \(\left( \alpha \right)\) qua \(A\) và \(B\) lần lượt cắt mặt phẳng \(\left( \alpha \right)\) tại \(A’\) và \(B’\). Chứng minh ba điểm \(A’, O, B’\) thẳng hàng và \(AA’ = BB’\).
Phương pháp giải - Xem chi tiết
- Chứng minh ba điểm \(O,A',B'\) cùng thuộc giao tuyến của \((AA’, BB’) \) với \(\left( \alpha \right)\).
- Chứng minh hai tam giác bằng nhau theo trường hợp cạnh huyền góc nhọn.
Lời giải chi tiết
\(\left\{ \matrix{
AA' \bot \left( \alpha \right) \hfill \cr
BB' \bot \left( \alpha \right) \hfill \cr} \right. \Rightarrow AA'\parallel BB'\)
Mặt phẳng \((AA’, BB’) \) xác định bởi hai đường thẳng song song \((AA’, BB’) \) cắt mặt phẳng \(\left( \alpha \right)\) theo giao tuyến qua \(O, A’, B’.\)
Do đó ba điểm \(O, A’, B’ \) thẳng hàng.
Hai tam giác vuông \(OAA’ \) và \(OBB’ \) bằng nhau vì có một cạnh huyền và một góc nhọn bằng nhau nên từ đó ta suy ra \(AA’ = BB’\).
soanvan.me
