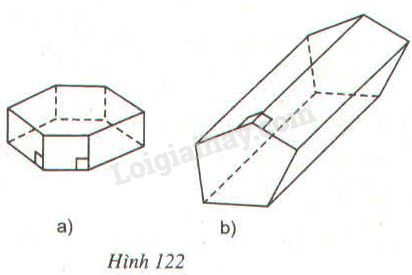
Quan sát các hình lăng trụ đứng trên hình 122 rồi điền số thích hợp vào các ô trống ở bảng dưới đây:
|
Hình lăng trụ |
Số cạnh của một đáy (n) |
Số mặt (m) |
Số đỉnh d |
Số cạnh c |
|
a) |
|
|
|
|
|
b) |
|
|
|
|
LG a
Viết các công thức liên hệ giữa \(n, m, d, c\).
Phương pháp giải:
Sử dụng: Công thức liên hệ giữa \(n, m, d, c\):
\(m = n + 2\); \(d = 2n\); \(c = 3n\).
Trong đó: \(n\) là số cạnh của một đáy
\(m\) là số mặt
\(d\) là số đỉnh
\(c\) là số cạnh.
Lời giải chi tiết:
|
Hình lăng trụ |
Số cạnh của một đáy (n) |
Số mặt (m) |
Số đỉnh d |
Số cạnh c |
|
a) |
6 |
8 |
12 |
18 |
|
b) |
5 |
7 |
10 |
15 |
a) Công thức liên hệ giữa \(n, m, d, c\):
\(m = n + 2\);
\(d = 2n\);
\(c = 3n\).
LG b
Hình lăng trụ đứng có \(20\) đỉnh thì có bao nhiêu mặt, bao nhiêu cạnh?
Phương pháp giải:
Sử dụng: Công thức liên hệ giữa \(n, m, d, c\):
\(m = n + 2\); \(d = 2n\); \(c = 3n\).
Trong đó: \(n\) là số cạnh của một đáy
\(m\) là số mặt
\(d\) là số đỉnh
\(c\) là số cạnh.
Lời giải chi tiết:
Số cạnh của một đáy là:
\(\displaystyle n = {d \over 2} = {{20} \over 2} = 10\) (cạnh)
Hình lăng trụ có \(20\) đỉnh, thì:
Số mặt là: \(m = n + 2 = 10 + 2 = 12\) (mặt)
Số cạnh là: \(c = 3n = 3.10 = 30\) (cạnh)
LG c
Có thể làm được một hình lăng trụ đứng có \(15\) đỉnh hay không?
Phương pháp giải:
Sử dụng: Công thức liên hệ giữa \(n, m, d, c\):
\(m = n + 2\); \(d = 2n\); \(c = 3n\).
Trong đó: \(n\) là số cạnh của một đáy
\(m\) là số mặt
\(d\) là số đỉnh
\(c\) là số cạnh.
Lời giải chi tiết:
Không thể làm một hình lăng trụ đứng có \(15\) đỉnh vì \(d = 2n\) (số đỉnh của lăng trụ là một số chẵn).
soanvan.me
