Đề bài
Một lăng trụ đứng lục giác đều có độ dài cạnh đáy là \(6cm\), chiều cao của lăng trụ là \(10 cm.\) Diện tích toàn phần của lăng trụ đó là (đơn vị cm2):
A. \(180 + 54\sqrt {3;} \)
B. \(180 + 108\sqrt {3;} \)
C. \(360 + 54\sqrt {3;} \)
D. \(360 + 108\sqrt {3.} \)
Hãy chọn kết quả đúng.
Phương pháp giải - Xem chi tiết
Sử dụng:
- Diện tích xung quanh của hình lăng trụ đứng bằng tổng diện tích các mặt bên hoặc bằng chu vi đáy nhân với chiều cao.
\({S_{xq}} = 2p.h\)
\(p\) là nửa chu vi đáy, \(h\) là chiều cao.
- Diện tích toàn phần của hình lăng trụ bằng tổng diện tích xung quanh và diện tích hai đáy.
- Diện tích một tam giác đều cạnh \(a\) là \(\dfrac{a^2.\sqrt 3}{4}\)
Lời giải chi tiết
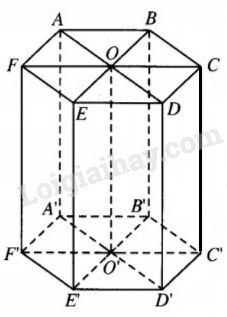
Nối các đường chéo \(AD, BE, CF\) của mặt đáy.
Các đường chéo chia lục giác ra thành \(6\) tam giác đều bằng nhau có cạnh là \(6\,(cm).\)
Diện tích mặt đáy bằng diện tích một tam giác đều cạnh \(6cm\) nhân với \(6\).
Diện tích một tam giác đều cạnh \(6cm\) là \(\dfrac{6^2.\sqrt 3}{4}=9\sqrt 3 (c{m^2})\)
Diện tích một mặt đáy là \(S_đ=6.9\sqrt 3=54\sqrt 3\; (c{m^2})\)
Diện tích xung quanh của hình lăng trụ là: \(S_{xq}=6.6.10 = 360\;(c{m^2})\)
Diện tích toàn phần của hình lăng trụ là:
\({S_{TP}} = {S_{xq}} + 2{S_đ}=360 + 2.54.\sqrt 3 \)\(\, = 360 + 108\sqrt 3\; (c{m^2})\)
Chọn D.
soanvan.me
