Đề bài
Trong tam giác vuông có một cạnh góc vuông bằng \(b\), góc đối diện với nó bằng \(β\).
a) Hãy biểu thị cạnh góc vuông kia, góc đối diện với cạnh này và cạnh huyền qua \(b\) và \(β\).
b) Hãy tìm các giá trị của chúng khi \(b = 10cm\), \(\beta = 50^\circ \) ( làm tròn kết quả đến chữ số thập phân thứ ba).
Phương pháp giải - Xem chi tiết
Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:

\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\)
Lời giải chi tiết
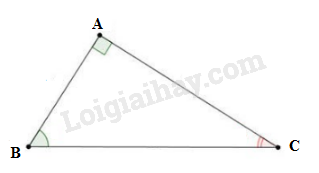
Trong tam giác \(ABC\) vuông tại \(A\), cạnh \(AC = b\), \(\widehat {ABC} = \beta \) thì:
a) Theo định nghĩa tỉ số lượng giác của góc nhọn ta có:
\(\begin{array}{l}
tg\beta = \dfrac{{AC}}{{AB}} = \dfrac{b}{{AB}} \Rightarrow AB = \dfrac{b}{{tg\beta }}\\
\cot g\beta = \dfrac{{AB}}{{AC}} = \dfrac{{AB}}{b} \Rightarrow AB = b.\cot g\beta
\end{array}\)
\(\sin \beta = \dfrac{{AC}}{{BC}} = \dfrac{b}{{BC}} \Rightarrow BC = \dfrac{b}{{\sin \beta }}\)
Vì tam giác ABC vuông tại A nên \(\widehat {ACB} = 90^\circ - \beta \)
b) Khi \(b = 10 (cm)\), \(\beta =50^\circ \) thì
\(AB = \dfrac{{10}}{{tg50^\circ }} \approx 8,391(cm),\) \(\widehat {ACB} = 90^0-50^0= 40^\circ ,\)\(BC = \dfrac{{10}}{{\sin 50^\circ }} \approx 13,054(cm).\)
soanvan.me
