Đề bài
Cho hình:
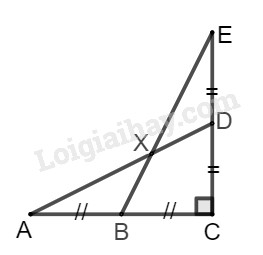
Biết:
\(\widehat {ACE} = 90^\circ, \)\(AB = BC = CD = DE = 2cm.\)
Hãy tính:
a) \(AD, BE;\)
b) \(\widehat {DAC}\);
c) \(\widehat {BXD}\).
Phương pháp giải - Xem chi tiết
+) Định lí Pytago vào tam giác \(ABC\) vuông tại \(A\):
\(A{B^2} + A{C^2} = B{C^2}.\)
+) Các tỉ số lượng giác của góc nhọn (hình) được định nghĩa như sau:

\(\sin \alpha = \dfrac{{AB}}{{BC}};\cos \alpha = \dfrac{{AC}}{{BC}};\)\(\tan \alpha = \dfrac{{AB}}{{AC}};\cot \alpha = \dfrac{{AC}}{{AB}}.\)
Lời giải chi tiết
a) Ta có:
\(AC = AB + BC = 2 + 2 = 4\left( {cm} \right)\)
Áp dụng định lí Pytago vào tam giác vuông \(ACD\), ta có:
\(A{D^2} = A{C^2} + C{D^2}\)\( = {4^2} + {2^2} = 16 + 4 = 20\)
\( \Rightarrow AD = \sqrt {20} = 2\sqrt 5 \left( {cm} \right)\)
Mặt khác: \(CE = CD + DE \)\(= 2 + 2 = 4\left( {cm} \right)\)
Áp dụng định lí Pytago vào tam giác vuông \(BEC\), ta có:
\(B{E^2} = B{C^2} + C{E^2}\)\( = {2^2} + {4^2} = 4 + 16 = 20\)
\( \Rightarrow BE = \sqrt {20} = 2\sqrt 5 \left( {cm} \right)\)
b) Tam giác \(ACD\) vuông tại \(C\) nên ta có:
\(\displaystyle tg\widehat {DAC} = {{CD} \over {AC}}\)\( = \dfrac{2 }{4} = \dfrac{1}{ 2}\)
Suy ra: \(\widehat {DAC} \approx 26^\circ 34'\)
c) Xét tam giác ADC vuông tại C, ta có: \(\widehat {CDA} = 90^\circ - \widehat {CAD}\)\( \approx 90^\circ - 26^\circ 34' = 63^\circ 26'\)
Xét hai tam giác ACD và ECB, ta có:
\(AC = EC \,(= 4cm)\)
\(BC = DC \,(= 2 cm)\)
\(AD = EB \,(= 2\sqrt 5 \left( {cm} \right))\)
Suy ra: \(ΔACD = ΔECB\) (c.c.c)
\(\Rightarrow \widehat {CBE}= \widehat {CDA} = 63^\circ 26'\)
Trong tứ giác \(BCDX,\) ta có:
\(\widehat {BXD} = 360^\circ - (\widehat C + \widehat {CDA} + \widehat {CBE})\)
\( = 360^\circ - (90^\circ + 63^\circ 26' + 63^\circ 26')\)\( = 143^\circ 8'.\)
soanvan.me
