Tính thể tích các khối tròn xoay tạo thành khi quay hình phẳng xác định bởi
LG câu a
\(\displaystyle y = {x^{\frac{2}{3}}},x = 0\) và tiếp tuyến với đường \(\displaystyle y = {x^{\frac{2}{3}}}\) tại điểm có hoành độ \(\displaystyle x = 1\), quanh trục \(\displaystyle Oy\);
Phương pháp giải:
- Viết phương trình tiếp tuyến của đồ thị hàm số \(\displaystyle y = {x^{\frac{2}{3}}}\) tại điểm có hoành độ bằng \(\displaystyle 1\).
- Rút \(\displaystyle x\) theo \(\displaystyle y\) và dựng hình rồi tính thể tích theo phương pháp cộng, trừ thể tích.
Chú ý: công thức \(\displaystyle V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \).
Giải chi tiết:
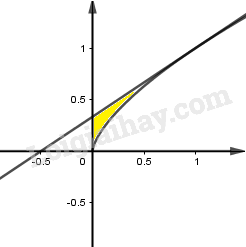
Ta có: \(\displaystyle y' = \frac{2}{3}{x^{ - \frac{1}{3}}}\).
Với \(\displaystyle x = 1\) thì \(\displaystyle y = 1\) và \(\displaystyle y'\left( 1 \right) = \frac{2}{3}\). Tiếp tuyến \(\displaystyle y = \frac{2}{3}\left( {x - 1} \right) + 1 = \frac{2}{3}x + \frac{1}{3}\)
Có \(\displaystyle y = {x^{\frac{2}{3}}} \Rightarrow x = {y^{\frac{3}{2}}}\) và \(\displaystyle y = \frac{2}{3}x + \frac{1}{3} \Rightarrow x = \frac{3}{2}y - \frac{1}{2}\)
Khi đó \(\displaystyle {y^{\frac{3}{2}}} = \frac{3}{2}y - \frac{1}{2} \Rightarrow y = 1\). Ta có: \(\displaystyle \frac{3}{2}y - \frac{1}{2} = 0 \Leftrightarrow y = \frac{1}{3}\)
\(\displaystyle V = \pi \int\limits_0^1 {{{\left( {{y^{\frac{3}{2}}}} \right)}^2}dy} - \pi \int\limits_{\frac{1}{3}}^1 {{{\left( {\frac{3}{2}y - \frac{1}{2}} \right)}^2}dy} \)\(\displaystyle = \pi \int\limits_0^1 {{y^3}dy} - \pi \int\limits_{\frac{1}{3}}^1 {{{\left( {\frac{3}{2}y - \frac{1}{2}} \right)}^2}dy} \)
\(\displaystyle = \pi .\left. {\frac{{{y^4}}}{4}} \right|_0^1 - \pi \int\limits_{\frac{1}{3}}^1 {\left( {\frac{9}{4}{y^2} - \frac{3}{2}y + \frac{1}{4}} \right)dy} \) \(\displaystyle = \frac{\pi }{4} - \pi .\left. {\left( {\frac{3}{4}{y^3} - \frac{3}{4}{y^3} + \frac{1}{4}y} \right)} \right|_{\frac{1}{3}}^1\) \(\displaystyle = \frac{\pi }{4} - \frac{{2\pi }}{9} = \frac{\pi }{{36}}\)
LG b
\(\displaystyle y = \frac{1}{x} - 1,y = 0,y = 2x\), quanh trục \(\displaystyle Ox\)
Phương pháp giải:
Dựng hình rồi tính thể tích theo phương pháp cộng, trừ thể tích.
Giải chi tiết:
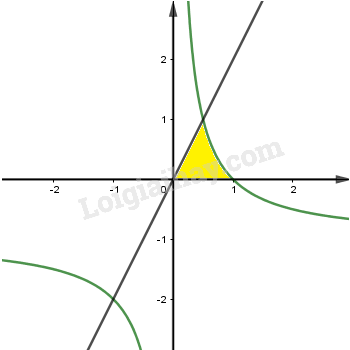
Ta có: \(\displaystyle \frac{1}{x} - 1 = 2x \Rightarrow x = \frac{1}{2}\); \(\displaystyle \frac{1}{x} - 1 = 0 \Leftrightarrow x = 1\); \(\displaystyle 2x = 0 \Leftrightarrow x = 0\).
Do đó \(\displaystyle V = \pi \int\limits_0^{\frac{1}{2}} {{{\left( {2x} \right)}^2}dx} + \pi \int\limits_{\frac{1}{2}}^1 {{{\left( {\frac{1}{x} - 1} \right)}^2}dx} \) \(\displaystyle = \pi .\int\limits_0^{\frac{1}{2}} {4{x^2}dx} + \pi .\int\limits_{\frac{1}{2}}^1 {\left( {\frac{1}{{{x^2}}} - \frac{2}{x} + 1} \right)dx} \)
\(\displaystyle = \pi .\left. {\frac{{4{x^3}}}{3}} \right|_0^{\frac{1}{2}} + \pi \left. {\left( { - \frac{1}{x} - 2\ln x + x} \right)} \right|_{\frac{1}{2}}^1\) \(\displaystyle = \frac{\pi }{6} + \pi \left( {0 + 2 + 2\ln \frac{1}{2} - \frac{1}{2}} \right)\) \(\displaystyle = \frac{\pi }{6} + \frac{{3\pi }}{2} - 2\pi \ln 2\)
\(\displaystyle = \frac{{5\pi }}{3} - 2\pi \ln 2\)
LG c
\(\displaystyle y = \left| {2x - {x^2}} \right|,y = 0\) và \(\displaystyle x = 3\), quanh:
* Trục \(\displaystyle Ox\)
* Trục \(\displaystyle Oy\)
Phương pháp giải:
Sử dụng công thức \(\displaystyle V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \).
Giải chi tiết:
+) Quay quanh \(\displaystyle Ox\).
Ta có: \(\displaystyle \left| {2x - {x^2}} \right| = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\).
Khi đó \(\displaystyle V = \pi \int\limits_0^3 {{{\left( {2x - {x^2}} \right)}^2}dx} \) \(\displaystyle = \pi \int\limits_0^3 {\left( {4{x^2} - 4{x^3} + {x^4}} \right)dx} \) \(\displaystyle = \pi \left. {\left( {\frac{{4{x^3}}}{3} - {x^4} + \frac{{{x^5}}}{5}} \right)} \right|_0^3\)
\(\displaystyle = \pi \left( {\frac{{4.27}}{3} - {3^4} + \frac{{{3^5}}}{5}} \right) = \frac{{18\pi }}{5}\).
+) Quay quanh \(\displaystyle Oy\).
Ta có: \(\displaystyle y = \left| {2x - {x^2}} \right|\) \(\displaystyle \Rightarrow \left[ \begin{array}{l}y = 2x - {x^2}\\y = - 2x + {x^2}\end{array} \right.\) \(\displaystyle \Leftrightarrow \left[ \begin{array}{l}{x^2} - 2x + y = 0\\{x^2} - 2x - y = 0\end{array} \right.\) \(\displaystyle \Leftrightarrow \left[ \begin{array}{l}x = 1 \pm \sqrt {1 - y} \\x = 1 \pm \sqrt {1 + y} \end{array} \right.\)
Dựng hình:
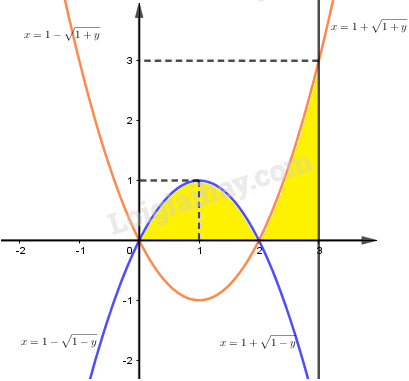
Ta có: \(\displaystyle {V_y} = \pi \int\limits_0^1 {\left[ {{{\left( {1 + \sqrt {1 - y} } \right)}^2} - {{\left( {1 - \sqrt {1 - y} } \right)}^2}} \right]dy} \) \(\displaystyle + \pi \int\limits_0^3 {\left[ {{3^2} - {{\left( {1 + \sqrt {1 + y} } \right)}^2}} \right]dy} \)
\(\displaystyle = \pi \int\limits_0^1 {\left( {1 + 2\sqrt {1 - y} + 1 - y - 1 + 2\sqrt {1 - y} - 1 + y} \right)dy} \)\(\displaystyle + \pi \int\limits_0^3 {\left( {9 - 1 - 2\sqrt {1 + y} - 1 - y} \right)dy} \)
\(\displaystyle = \pi \int\limits_0^1 {4\sqrt {1 - y} dy} \) \(\displaystyle + \pi \int\limits_0^3 {\left( {7 - y - 2\sqrt {1 + y} } \right)dy} \)
\(\displaystyle = 4\pi \int\limits_0^1 {\sqrt {1 - y} dy} \) \(\displaystyle + \pi \left[ {\left. {\left( {7y - \frac{{{y^2}}}{2}} \right)} \right|_0^3 - 2\int\limits_0^3 {\sqrt {1 + y} dy} } \right]\) \(\displaystyle = 4\pi I + \pi \left( {\frac{{33}}{2} - 2J} \right)\)
Tính \(\displaystyle I = \int\limits_0^1 {\sqrt {1 - y} dy} \) ta có:
Đặt \(\displaystyle \sqrt {1 - y} = t \Rightarrow 1 - y = {t^2}\) \(\displaystyle \Rightarrow - dy = 2tdt \Rightarrow dy = - 2tdt\)
\(\displaystyle \Rightarrow I = \int\limits_1^0 {t.\left( { - 2tdt} \right)} \) \(\displaystyle = \int\limits_0^1 {2{t^2}dt} = \left. {\frac{2}{3}{t^3}} \right|_0^1 = \frac{2}{3}\)
Tính \(\displaystyle J = \int\limits_0^3 {\sqrt {1 + y} dy} \) ta có:
Đặt \(\displaystyle t = \sqrt {1 + y} \Rightarrow {t^2} = 1 + y\) \(\displaystyle \Rightarrow 2tdt = dy\) \(\displaystyle \Rightarrow J = \int\limits_1^2 {t.2tdt} = \left. {\frac{{2{t^3}}}{3}} \right|_1^2 = \frac{{14}}{3}\)
Vậy \(\displaystyle V = 4\pi .\frac{2}{3} + \pi \left( {\frac{{33}}{2} - 2.\frac{{14}}{3}} \right) = \frac{{59\pi }}{6}\).
soanvan.me
