Đề bài
Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, \(\widehat {HCA} = 25^\circ \). Tính \(\widehat {BAC}\)và \(\widehat {HBA}\).
Phương pháp giải - Xem chi tiết
Tổng hai góc nhọn trong một tam giác vuông bằng 90°.
Lời giải chi tiết
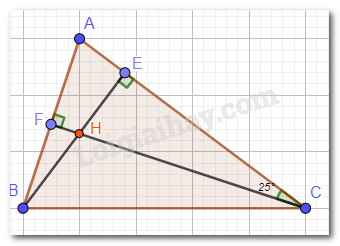
Xét tam giác AFC có: \(\widehat {HCA} = 25^\circ \); \(\widehat {AFC} = 90^\circ \) (vì CF vuông góc với AB).
Nên: \(\widehat {FAC} = \widehat {BAC} = 90^\circ - 25^\circ = 65^\circ \).
Xét tam giác AEB có: \(\widehat {BAC} = 65^\circ \); \(\widehat {AEB} = 90^\circ \)(vì BE vuông góc với AC).
Nên: \(\widehat {ABE} = \widehat {HBA} = 90^\circ - 65^\circ = 25^\circ \).
