Đề bài
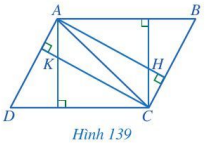
Trong Hình 139, cho biết AB // CD, AD // BC; H, K lần lượt là trực tâm các tam giác ABC và ACD. Chứng minh AK // CH và AH // CK.
Phương pháp giải - Xem chi tiết
Áp dụng tính chất:
+ Nếu \(a//b; a \bot c \) thì \(b \bot c\)
+ Nếu \(a \bot c; b \bot c\) thì \(a//b\)
Lời giải chi tiết
Vì AD // BC, mà K \(\in\) AD, H \(\in\) BC nên AK // CH
Vì \(CK \bot AD; BC // AD\) nên \(CK \bot BC\)
Mà \(AH \bot BC\)
\(\Rightarrow AH // CK\)
