Video hướng dẫn giải
Để trang hoàng cho căn hộ của mình, chú chuột Mickey quyết định tô màu một miếng bìa hình vuông cạnh bằng \(1\). Nó tô màu xám các hình vuông nhỏ được đánh dấu \(1, 2, 3, ..., n, ...\) trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó (h.51)
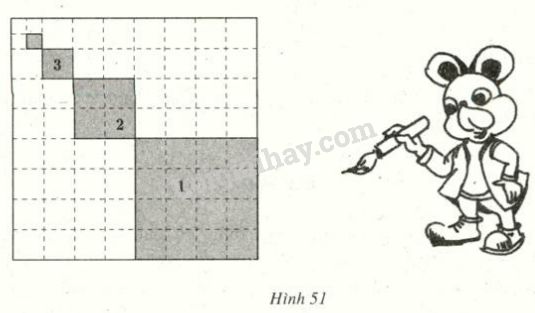
Giả sử quy trình tô màu của Mickey có thể tiến ra vô hạn.
LG a
Gọi \(u_n\) là diện tích của hình vuông màu xám thứ \(n\). Tính \(u_1, u_2, u_3\) và \(u_n\).
Phương pháp giải:
Tính diện tích của hình vuông \(S=a^2\) với \(a\) là cạnh của hình vuông.
Lời giải chi tiết:
Do hình vuông lớn có cạnh bằng 1, hình vuông màu xám thứ nhất có cạnh bằng một nửa cạnh hình vuông lớn nên:
Hình vuông thứ nhất có cạnh bằng \(\dfrac{1}{2}\) nên \({u_1} = {\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{4^1}\).
Hình vuông thứ hai có cạnh bằng \(\dfrac{1}{4}\) nên \(\displaystyle{u_2} = {\left( {{1 \over 4}} \right)^2} = {1 \over {{4^2}}}\).
Hình vuông thứ ba có cạnh bằng \(\dfrac{1}{8}\) nên \(\displaystyle{u_3} = {\left( {{1 \over 8}} \right)^2} = {1 \over {{4^3}}}\)
Tương tự, ta có \(u_n=\dfrac{1}{4^{n}}\)
LG b
Tính \(\lim S_n\) với \(S_n= {u_{1}} + {u_{2}} + {u_{3}} + ... + {u_{n}}\)
Phương pháp giải:
Sử dụng công thức tổng của cấp số nhân lùi vô hạn \(S = \dfrac{{{u_1}}}{{1 - q}}\,\,\left( {\left| q \right| < 1} \right)\).
Lời giải chi tiết:
Dãy số \((u_n)\) là một cấp số nhân lùi vô hạn với \(u_1=\dfrac{1}{4}\) và \(q = \dfrac{1}{4}\). Do đó
\(\lim S_n=\dfrac{u_{1}}{1-q}= \dfrac{\dfrac{1}{4}}{1-\dfrac{1}{4}}=\dfrac{1}{3}\).
soanvan.me
