Video hướng dẫn giải
Cho biết \(\dfrac{AB'}{AB} = \dfrac{AC'}{AC}\) (h.6)
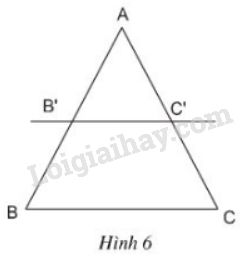
Chứng minh rằng:
LG a.
\(\dfrac{AB'}{B'B}= \dfrac{AC'}{C'C}\)
Phương pháp giải:
- Áp dụng định lí TaLet và tính chất dãy tỉ số bằng nhau.
Lời giải chi tiết:
Ta có:
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\) (giả thiết)
\( \Rightarrow \dfrac{AC}{AC'}=\dfrac{AB}{AB'}\)
\( \Rightarrow \dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AB}}{{AB'}} - 1\)
Ta có:
\(\dfrac{{AC}}{{AC'}} - 1 = \dfrac{{AC - AC'}}{{AC'}} = \dfrac{{C'C}}{{AC'}}\)
\(\dfrac{{AB}}{{AB'}} - 1 = \dfrac{{AB - AB'}}{{AB'}} = \dfrac{{B'B}}{{AB'}}\)
\( \Rightarrow \dfrac{{C'C}}{{AC'}} = \dfrac{{B'B}}{{AB'}} \Rightarrow \dfrac{{AB'}}{{B'B}} = \dfrac{{AC'}}{{C'C}}\) (điều phải chứng minh).
LG b.
\(\dfrac{BB'}{AB} = \dfrac{CC'}{AC}\).
Phương pháp giải:
- Áp dụng định lí TaLet và tính chất dãy tỉ số bằng nhau.
Lời giải chi tiết:
Vì \(\dfrac{AB'}{AB} = \dfrac{AC'}{AC}\)
Mà \(AB' = AB - B'B, AC' = AC - C'C\)
\(\dfrac{AB-BB'}{AB} = \dfrac{AC -CC'}{AC}\)
\( \Rightarrow 1 - \dfrac{{BB'}}{{AB}} = 1 - \dfrac{{CC'}}{{AC}}\)
\( \Rightarrow \dfrac{BB'}{AB}= \dfrac{CC'}{AC}\) (điều phải chứng minh).
soanvan.me
