Đề bài
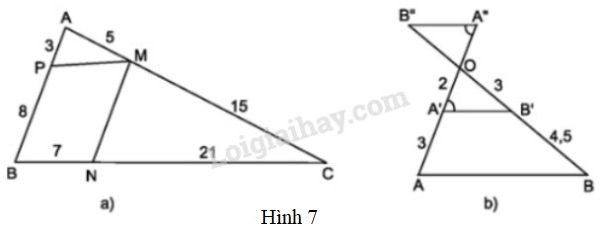
Tìm các cặp đường thẳng song song trong hình 7 và giải thích vì sao chúng song song.
Phương pháp giải - Xem chi tiết
- Áp dụng định lý TaLet đảo: Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
- Dấu hiệu nhận biết hai đường thẳng song song.
Lời giải chi tiết
a) Xét \(\Delta ABC\) và đường thẳng \(PM\) (h.7a) ta thấy:
\(\dfrac{AP}{PB} = \dfrac{3}{8}\); \(\dfrac{AM}{MC}= \dfrac{5}{15} = \dfrac{1}{3}\); \(\dfrac{3}{8} ≠ \dfrac{1}{3}\)
Suy ra \(PM\) không song song với \(BC\).
Xét \(\Delta ABC\) và đường thẳng \(MN\) (h.7a) ta thấy:
\(\dfrac{{AM}}{{MC}} = \dfrac{5}{{15}};\dfrac{{BN}}{{NC}} = \dfrac{7}{{21}};\dfrac{5}{{15}} = \dfrac{7}{{21}}\)
Vậy \(\dfrac{{AM}}{{MC}} = \dfrac{{BN}}{{NC}}\)
Áp dụng định lí Ta - lét đảo, suy ra \( MN// AB\).
b) So sánh các góc so le trong, ta thấy \(\widehat {B''A''A'} = \widehat {A''A'B'}\) (h.7b)
Vậy \(A'B'//A''B''\).
Xét \(\Delta AOB\) và đường thẳng \(A'B'\), ta thấy:
\(\dfrac{OA'}{A'A} = \dfrac{2}{3}\); \(\dfrac{OB'}{B'B} = \dfrac{3}{4,5} ;\) \( \dfrac{2}{3} = \dfrac{3}{4,5} .\)
Vậy: \( \dfrac{OA'}{A'A} = \dfrac{OB'}{B'B}\)
Áp dụng định lí TaLet đảo, suy ra \(A'B' // AB\).
Từ các kết quả trên, ta có: \(A''B''//A'B'//AB\).
soanvan.me
