Tính các độ dài \(x,y\) trong hình 8.
LG a
Phương pháp giải:
- Áp dụng: hệ quả của định lý TaLet, định lý Pitago.
Lời giải chi tiết:
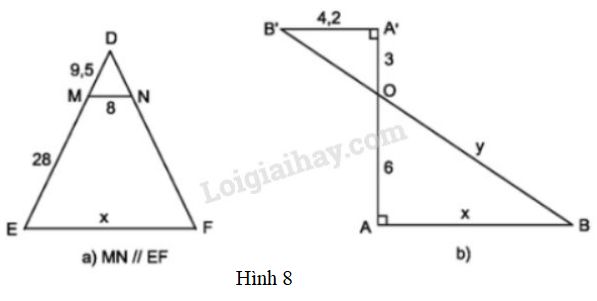
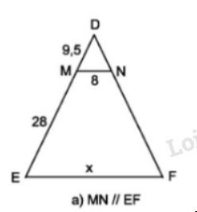
\(MN // EF\) (h.8a). Theo hệ quả định lí Ta-lét ta có:
\(\frac{{DM}}{{DE}} = \frac{{MN}}{{EF}}\) hay \( \dfrac{9,5}{(9,5+28)}=\dfrac{8}{x} \)
Vậy \( x= \dfrac{8.(9,5+28)}{9,5}\)
Tính trên máy tính bỏ túi, ta được \(x ≈ 31,57894737\).
Lấy chính xác đến hai chữ số thập phân, ta có: \(x ≈ 31,58\).
LG b
Phương pháp giải:
- Áp dụng: hệ quả của định lý TaLet, định lý Pitago.
Lời giải chi tiết:
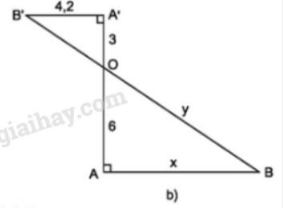
\(A'B' ⊥ AA';\;AB ⊥ AA'\) (h.8b)
Suy ra \(A'B' // AB\).
Theo hệ quả của định lí Ta - lét, ta có:
\( \dfrac{OA'}{OA} = \dfrac{A'B'}{AB}\) hay \(\dfrac{3}{6} = \dfrac{4,2}{x}\)
\(x = \dfrac{4,2.6}{3} = 8,4\)
Xét tam giác vuông \(OAB\):\( O{B^2} = O{A^2} + A{B^2} \)
hay \({y^2} = {6^2} + 8,{4^2} = 106,56\)
Suy ra \(y = \sqrt {106,56}\)
Tính trên máy tính bỏ túi được: \(y\approx 10,32279032\).
Lấy chính xác đến hai chữ số thập phân, ta được: \(y\approx 10,32\).
soanvan.me
