Đề bài
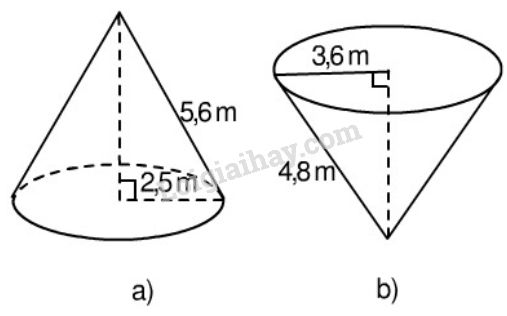
Hãy tính diện tích toàn phần của các hình tương ứng theo các kích thước đã cho trên hình 115.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Diện tích xung quanh của hình nón: \(S_{xq}=\pi rl.\)
+) Diện tích toàn phần của hình nón: \(S_{tp}=\pi rl + \pi r^2.\)
Lời giải chi tiết
- Với hình a: Hình nón có bán kính đáy r = 2,5m, đường sinh l = 5,6m
\({S_{tp}} = {\rm{ }}{S_{xq}} + {\rm{ }}{S_{đáy}} = {\rm{ }}\pi rl{\rm{ }} + {\rm{ }}\pi {r^2}\)
\(= {\rm{ }}\pi {\rm{ }}.{\rm{ }}2,5{\rm{ }}.{\rm{ }}5,6{\rm{ }} + {\rm{ }}\pi {\rm{ }}.{\rm{ }}2,{5^2} \approx {\rm{ }}63,59{\rm{ }}({m^2})\)
- Với hình b: Hình nón có bán kính đáy r = 3,6m; đường sinh l = 4,8m
\({S_{tp}} = {\rm{ }}{S_{xq}} + {\rm{ }}{S_{đáy}} = {\rm{ }}\pi {\rm{ }}.{\rm{ }}3,6{\rm{ }}.{\rm{ }}4,8{\rm{ }} + {\rm{ }}\pi {\rm{ }}.{\rm{ }}3,{6^2} \)
\( \approx {\rm{ }}94,95{\rm{ }}({m^2})\)
