Đề bài
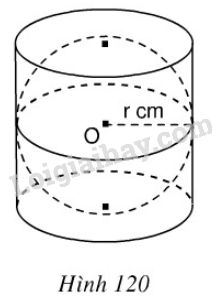
Hình 120 mô tả một hình cầu được đặt khít vào trong một hình trụ, các kích thước cho trên hình vẽ.
Hãy tính:
a)Thể tích hình cầu.
b) Thể tích hình trụ.
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu.
d) Thể tích của một hình nón có bán kính đường tròn đáy là \(r \, (cm)\) và chiều cao \(2r\, (cm)\).
e) Từ các kết quả a), b), c), d) hãy tìm mối liên hệ giữa chúng.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
+) Thể tích hình trụ: \(V=\pi r^2 h.\)
+) Thể tích hình nón: \(V = \dfrac{1}{3}\pi {r^2}h.\)
+) Thể tích hình cầu: \(V = \dfrac{4}{3}\pi {r^3}.\)
Lời giải chi tiết
a) Thể tích của hình cầu bán kính r cm là: \(\displaystyle {V_1} = {4 \over 3}\pi {r^3}(c{m^3})\)
b) Theo hình vẽ, hình trụ có chiều cao là: \(h=2r.\) cm
\(\Rightarrow \) Thể tích hình trụ chiều cao h =2r cm, bán kính đáy r cm là: \({V_2} = {\rm{ }}\pi {r^2}.{\rm{ }}2r{\rm{ }} = {\rm{ }}2\pi {r^3}(c{m^3})\)
c) Hiệu giữa thể tích hình trụ và thể tích hình cầu là:
\(\displaystyle {V_3} = {V_2} - {V_1} = 2\pi {r^3} - {4 \over 3}\pi {r^2} = {2 \over 3}\pi {r^3}(c{m^3})\)
d) Thể tích hình nón bán kính đường tròn đáy là \(r \, (cm)\) và chiều cao \(2r\, (cm)\) là:
\(\displaystyle {V_4} = {\pi \over 3}{r^2}.2{\rm{r}} = {2 \over 3}\pi {r^3}(c{m^3})\)
e) Từ kết quả ở câu a, b,c, d ta có: \({V_4} = {\rm{ }}{V_2}-{\rm{ }}{V_1}\) hay “ Thể tích hình nón nội tiếp trong hình trụ bằng hiệu giữa thể tích hình trụ và thể tích hình cầu nội tiếp trong hình trụ ấy”
Hoặc "Thể tích hình trụ bằng tổng thể tích nón và hình cầu nội tiếp trong hình trụ đó".
