Video hướng dẫn giải
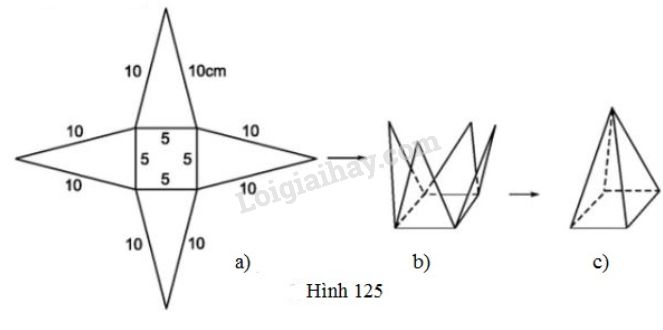
Vẽ cắt và gấp miếng bìa như đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.
LG a.
Trong hình 125a, có bao nhiêu tam giác cân bằng nhau?
Phương pháp giải:
Áp dụng: Định nghĩa chóp tứ giác đều
Giải chi tiết:
Trong hình 125a có 4 tam giác cân bằng nhau.
LG b.
Sử dụng định lí Pitago để tính chiều cao ứng với đáy của mỗi tam giác.
Phương pháp giải:
Áp dụng: Định lý Py-ta-go
Giải chi tiết:
Đặt tên cho 1 mặt bên như hình vẽ:
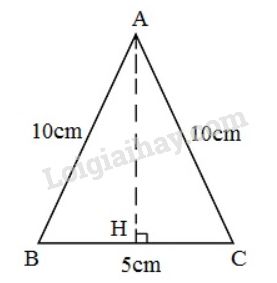
Gọi H là chân đường cao hạ từ A xuống BC, mà tam giác ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến.
Do đó \(HC=BC:2=\dfrac{5}{2}cm\)
Xét tam giác AHC vuông tại H, theo định lý Py-ta-go ta có:
\(AH = \sqrt{AC^{2}- HC^{2}}\)
\(= \sqrt{10^{2}- {\left( {\dfrac{5}{2}} \right)^2}} = \sqrt{100-\dfrac{25}{4}} \)
\(\approx 9,68\) \(cm\)
LG c.
Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu ?
Phương pháp giải:
Áp dụng:
- Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn.
- Công thức tính diện tích toàn phần: \( S_ {tp} = S_{xq}+ S_{đ}\)
Giải chi tiết:
Chu vi đáy của hình chóp là \(4.5 = 20 (cm).\)
Diện tích xung quanh hình chóp:
\(S_{xq} = p. d =\dfrac{1}{2}.20.9,68 = 96,8\) \( (cm^2) \)
Diện tích đáy:
\( S_{đ} = 5^2 = 25 (cm^2) \)
Diện tích toàn phần của hình chóp:
\( S_ {tp} = S_{xq}+ S_{đ} = 96,8 + 25 = 121,8\) \((cm^2) \)
soanvan.me
