Đề bài
Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho ở hình 125.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lý Pytago trong tam giác vuông.
Lời giải chi tiết
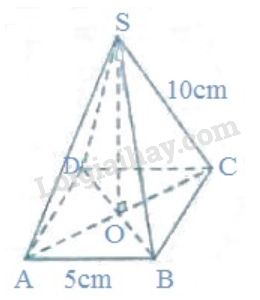
Gọi tên như hình vẽ.
Gọi \(O\) là giao điểm hai đường chéo của hình vuông đáy. Khi đó SO là chiều cao của hình chóp tứ giác đều. Ta đi tính SO.
Tam giác \(ABC\) vuông tại \(B\) nên theo định lý Pytago, ta có :
\( AC^2 = AB^2 + BC^2 \)\(\,= 5^2 + 5^2 = 50 \)
Vì ABCD là hình vuông nên O là trung điểm của AC. Suy ra \(OC=\dfrac{AC}{2}\)
Tam giác \(SOC\) vuông tại \(O\) nên theo định lý Pytago, ta có:
\( SO^2 + OC^2 = SC^2\)
\( \Rightarrow SO^2 = SC^2 - OC^2 \)\(\,= SC^2 - {\left( {\dfrac{{AC}}{2}} \right)^2}\)
\( SO = \sqrt{SC^{2}- {\left( {\dfrac{{AC}}{2}} \right)^2}}\)\(\,= \sqrt{10^{2}- \dfrac{50}{4}}\) \(\approx 9,35\, (cm)\)
