Đề bài
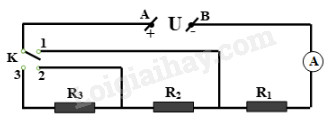
Đặt một hiệu điện thế U vào hai đầu một đoạn mạch có sơ đồ như trên hình 4.5. Khi đóng công tắc K vào vị trí 1 thì ampe kế có số chỉ \(I_1 = I\), khi chuyển công tắc này sang vị trí số 2 thì ampe kế có số chỉ là \({I_2} = \dfrac{I}{3}\) , còn khi chuyển K sang vị trí 3 thì ampe kế có số chỉ \(I_3 =\dfrac{I}{8}\) . Cho biết \( R_1 = 3Ω\), hãy tính \(R_2\) và \(R_3\).
Phương pháp giải - Xem chi tiết
+ Sử dụng biểu thức: \(U=I.R\)
+ Sử dụng biểu thức: \(R_{tđ} = {R_1} + {R_2} + {R_3}\)
Lời giải chi tiết
+) Khi K đóng ở vị trí 1: \(I_1 = I; R_{tđ}=R_1= 3\Omega\) (1)
+) Khi K đóng ở vị trí 2 : \({I_2} = \dfrac{I}{3}; R_{tđ} = {R_1} + {R_2} = 3 + {R_2}\) (2)
+) Khi K đóng ở vị trí 3: \(I_3 = \dfrac{I}{8}\)
\(R_{tđ} = {R_1} + {R_2} + {R_3} = 3 + {R_2} + {R_3}\) (3)
Từ (1) \(\Rightarrow U = {I_1}.{R_1} = 3I\) (1’)
Từ (2) \(\Rightarrow U = {I_2}(3 + {R_2}) = \dfrac{I}{3}(3 + {R_2})\) (2’)
Từ (3) \(\Rightarrow U = {I_3}(3 + {R_2} + {R_3}) =\dfrac{I}{8}(3 + {R_2} + {R_3})\) (3’)
Thay (1’) và (2’) \(\Rightarrow 3I =\dfrac{I}{3}(3 + {R_2}) \Rightarrow {R_2} = 6\Omega\)
Thay (1’) và R2 vào (3’) \(\Rightarrow 3I = \dfrac{I}{8}(3 + 6 + {R_3}) \Rightarrow {R_3} = 15\Omega \)
Vậy \( R_2=6\Omega\); \(R_3=15\Omega\)
