Đề bài
Cho điểm \(A\) nằm ngoài đường thẳng \(d\) và có khoảng cách đến \(d\) bằng \(2cm\). lấy điểm \(B\) bất kì thuộc đường thẳng \(d\). Gọi \(C\) là điểm đối xứng với điểm \(A\) qua điểm \(B\). Khi điểm \(B\) di chuyển trên đường thẳng \(d\) thì điểm \(C\) di chuyển trên đường nào ?
Phương pháp giải - Xem chi tiết
Áp dụng:
+) Hai điểm \(A\) và \(A'\) gọi là đối xứng nhau qua điểm \(O\) nếu \(O\) là trung điểm của \(AA'.\)
+) Tính chất: Các điểm cách đường thẳng \(b\) một khoảng bằng \(h\) nằm trên hai đường thẳng song song với \(b\) và cách \(b\) một khoảng bằng \(h.\)
Lời giải chi tiết
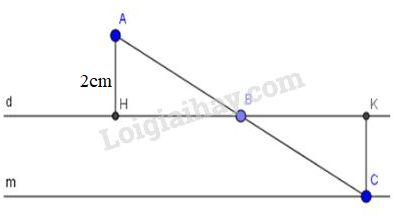
Kẻ \(AH\bot d,\) \(CK\bot d\)
Các tam giác vuông \(AHB\) và \(CKB\) có: \(AB = CB\) (vì \(C\) đối xứng với \(A\) qua \(B\)), \(\widehat{ABH} = \widehat{CBK}\) ( đối đỉnh)
Do đó \(∆AHB = ∆CKB\) suy ra \(CK = AH = 2cm\) (\(2\) cạnh tương ứng)
Điểm \(C\) cách đường thẳng \(d\) một khoảng bằng \(2cm\) nên \(C\) di chuyển trên đường thẳng \(m\) song song với \(d\) và cách \(d\) một khoảng bằng \(2cm\).
soanvan.me
