Đề bài
Cho tam giác \(ABC\) vuông tại \(A\). Lấy \(M\) là một điểm bất kì thuộc cạnh \(BC\). Gọi \(MD\) là đường vuông góc kẻ từ \(M\) đến \(AB\), \(ME\) là đường vuông góc kẻ từ \(M\) đến \(AC\), \(O\) là trung điểm của \(DE\).
a) Chứng mình rằng ba điểm \(A, O, M\) thẳng hàng.
b) Khi điểm \(M\) di chuyển trên cạnh \(BC\) thì điểm \(O\) di chuyển trên đường nào ?
c) Điểm \(M\) ở vị trí nào trên cạnh \(BC\) thì \(AM\) có độ dài nhỏ nhất?
Phương pháp giải - Xem chi tiết
Sử dụng: Đường trung bình của tam giác thì song song với cạnh thứ 3 và bằng nửa độ dài cạnh ấy.
Lời giải chi tiết
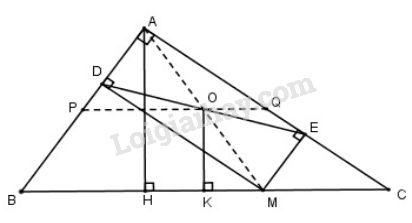

a) Tứ giác \(ADME\) có: \(\widehat {A} = {90^0}\) (giả thiết), \(\widehat D = {90^o}\) (vì \(MD\bot AB\)), \(\widehat E = {90^o}\) (vì \(ME\bot AC\)) nên là hình chữ nhật.
Vì \(O\) là trung điểm của \(DE\) nên \(O\) cũng là trung điểm của \(AM\). Do đó \(A, O, M\) thẳng hàng.
b) Kẻ \(AH ⊥ BC\), \(OK ⊥ BC\), ta có \(OK // AH\) (do cùng vuông góc với \(BC\)).
Tam giác \(AHM\) có \(OA=OM\) và \(OK // AH\) nên \(OK\) là đường trung bình, suy ra \(OK =\dfrac{1}{2}AH\)
Điểm \(O\) cách \(BC\) một khoảng không đổi bằng \(\dfrac{1}{2}AH\) nên \(O\) di chuyển trên đường thẳng song song với \(BC\) và cách \(BC\) một khoảng bằng \(\dfrac{1}{2}AH\)
Gọi giao điểm của đường thẳng đó với \(AB, AC\) théo thứ tự \(P,Q\). Vì \(M\) chỉ di chuyển trên cạnh \(BC\) nên \(O\) chỉ di chuyển trên đoạn thẳng \(PQ\)
Lưu ý: Điểm \(P\) là trung điểm của \(AB\), điểm \(Q\) là trung điểm của \(AC\).
soanvan.me
