Đề bài
Trên mặt phẳng tọa độ Oxy hãy vẽ các vecto \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) với A (1; 2), M (0; -1), N (3; 5).
a) Chỉ ra mỗi quan hệ giữa hai vecto trên.
b) Một vật thể khởi hành từ M chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn vởi vecto \(\overrightarrow v = \overrightarrow {OA} \). Hỏi vật thể đó có đi qua N hay không? Nếu có thì sau bao lâu sẽ tới N?
Lời giải chi tiết
a)
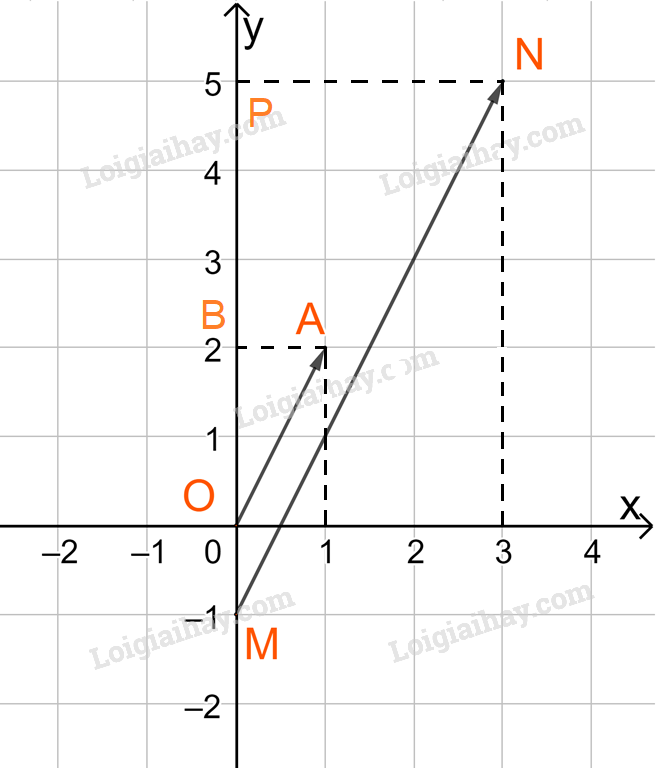
Lấy điểm B(0;2) và P(0;5).
Ta có: OB=2, AB =1, MP=6 và PN=3.
Xét hai tam giác vuông OBA và MPN ta có: \(\frac{{OB}}{{MP}} = \frac{{AB}}{{PN}} = \frac{1}{3}\)
Do đó hai tam giác đồng dạng và OA // MN.
Suy ra \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) cùng phương.
Hơn nữa, \(\overrightarrow {OA} ,\;\overrightarrow {MN} \) cùng hướng và MN = 3 OA.
b) Mỗi giờ, vật thể đó đi được quãng đường tương ứng với đoạn thẳng OA.
Vì \({MN} = 3. {OA} \) nên vật thể đó sẽ đi qua N sau 3 giờ kể từ lúc khởi hành.
