Đề bài
Cho một đa giác đều \(n\) cạnh có độ dài mỗi cạnh là \(a.\) Hãy tính bán kính \(R\) của đường tròn ngoại tiếp và bán kính \(r\) của đường tròn nội tiếp đa giác đều đó.
Hướng dẫn:
Tính \(\widehat {COB}\) rồi tính \(\sin \widehat {COB}\) và \(\tan\widehat {COB},\) từ đây tính được \(R\) và \(r\) \((h.4).\)
Phương pháp giải - Xem chi tiết
Ta sử dụng kiến thức:
+) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác.
+) Đường tròn tiếp xúc với tất cả các cạnh của đa giác được gọi là đường tròn nội tiếp đa giác.
+) Số đo góc ở tâm chắn mỗi cạnh của đa giác đều \(n\) cạnh bằng \(\dfrac{360^\circ}{n}.\)
Lời giải chi tiết
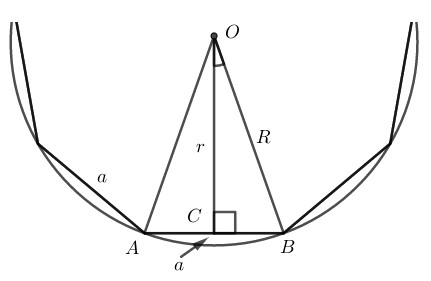
Giả sử một đa giác đều \(n\) cạnh có độ dài một cạnh là \(a.\) Gọi \(R\) là bán kính đường tròn ngoại tiếp, \(r\) bán kính đường tròn nội tiếp.
\( \Rightarrow OB = R; OC = r\)
\(\widehat {AOB} = \displaystyle{{360^\circ } \over n}\)
\( \Rightarrow \widehat {COB} = \displaystyle{{360^\circ } \over n}:2 = {{180^\circ } \over n}\)
Trong \(∆OCB\) ta có: \(\widehat {OCB} = 90^\circ \)
Nên \(\sin \widehat {COB} = \displaystyle{{CB} \over {OB}} = {\displaystyle{{a \over 2}} \over R} = {a \over {2R}}\)
\( \Rightarrow 2R = \displaystyle{a \over {\sin \displaystyle{{180^\circ } \over n}}}\)
\(\Rightarrow R =\displaystyle {a \over {2\sin \displaystyle{{180^\circ } \over n}}}\)
Xét tam giác \(OCB\) vuông tại \(C\), ta có:
\(\tan \widehat {COB} = \displaystyle{{CB} \over {OC}} = {\displaystyle{{a \over 2}} \over r} = \displaystyle{a \over {2r}} \)
\(\Rightarrow 2r = \displaystyle{a \over {\tan \displaystyle{{180^\circ } \over n}}}\)
\(\Rightarrow r = \displaystyle{a \over {2\tan \displaystyle{{180^\circ } \over n}}}\)
soanvan.me
