Đề bài
Cho tam giác ABC. Gọi I là trung điểm của BC. Tính số đo góc BAC, biết IA = IB = IC.
Phương pháp giải - Xem chi tiết
- Tam giác IAB, IAC cân tại I nên suy ra các góc ở đáy bằng nhau.
- Tổng ba góc trong một tam giác bằng \({180^o}\).
- Tính số đo góc BAC.
Lời giải chi tiết
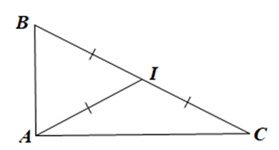
• Vì IA = IB nên tam giác IAB cân tại I.
Suy ra \(\widehat {IBA} = \widehat {IAB}\)
• Vì IA = IC nên tam giác IAC cân tại I.
Suy ra \(\widehat {IAC} = \widehat {ICA}\)
Xét ∆ABC có: \(\widehat {BAC} + \widehat {CBA} + \widehat {BCA} = 180^\circ \) (tổng ba góc của một tam giác).
Hay \(\widehat {BAC} + \widehat {IAB} + \widehat {IAC} = 2\widehat {BAC} = 180^\circ \)
Do đó \(\widehat {BAC} = 90^\circ \)
Vậy \(\widehat {BAC} = 90^\circ \)
