Đề bài
Cho tam giác đều ABC. Gọi E, D, F là ba điểm lần lượt nằm trên ba cạnh AB, AC, BC sao cho AD = CF = BE. Chứng minh tam giác DEF là tam giác đều.
Phương pháp giải - Xem chi tiết
Chứng minh: DE = EF = FD suy ra tam giác DEF đều.
Lời giải chi tiết
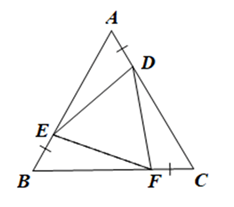
Vì tam giác ABC đều (giả thiết)
Nên AB = BC = AC và \(\widehat {ABC} = \widehat {BAC} = \widehat {ACB} = 60^\circ \)
Ta có AB = AE + BE, AC = AD + DC, BC = BF + FC
Mà AB = BC = AC, AD = CF = BE.
Suy ra AE = BF = CD.
• Xét ∆ADE và ∆BEF có:
AD = BE (giả thiết),
\(\widehat {DAE} = \widehat {FBE}\) (cùng bằng 60°),
AE = BF (chứng minh trên).
Do đó ∆ADE = ∆BEF (c.g.c).
Suy ra DE = EF (hai cạnh tương ứng) (1)
• Xét ∆CFD và ∆BEF có:
CF = BE (giả thiết),
\(\widehat {FCD} = \widehat {EBF}\) (cùng bằng 60°),
CD = BF (chứng minh trên).
Do đó ∆CFD = ∆BEF (c.g.c).
Suy ra FD = EF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra DE = EF = FD.
Do đó tam giác DFE đều.
Vậy tam giác DEF là tam giác đều.
