Đoán nhận số nghiệm của các hệ phương trình sau bằng hình học:
Chú ý: Trong bài này, ta cần xét vị trí tương đối của hai đường thẳng (để suy ra số nghiệm của hệ phương trình) bằng cách vẽ hai đường thẳng đó.
LG a
\(\left\{ \begin{array}{l}2x - y = 1\\x - 2y = - 1\end{array} \right.\)
Phương pháp giải:
Xét hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\,\,\,\,\,\,\,\,\,\,(1)\\a'x + b'y = c'\,\,\,(2)\end{array} \right.\) có \(d\) là đường thẳng biểu diễn tập nghiệm của phương trình \(\left( 1 \right)\) và \(d'\) là đường thẳng biểu diễn tập nghiệm của phương trình \(\left( 2 \right)\), khi đó ta vẽ hai đường thẳng \(d\) và \(d'\) trên cùng hệ trục tọa độ để xác định số giao điểm của \(d\) và \(d'\) .
Từ đó suy ra số nghiệm của hệ đã cho.
Lời giải chi tiết:
Vẽ các đường thẳng \(2x - y = 1;\,x - 2y = - 1\) trong cùng một hệ tọa độ (h.7)
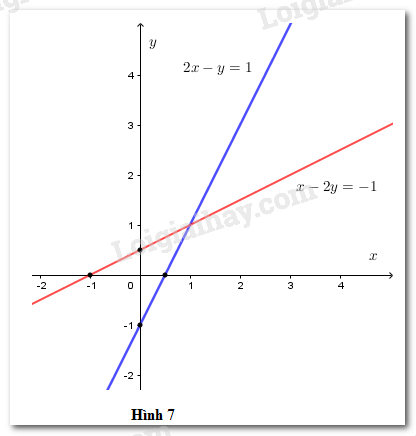
Ta thấy hai đường thẳng này cắt nhau tại một điểm.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
LG b
\(\left\{ \begin{array}{l}2x + y = 4\\ - x + y = 1\end{array} \right.\)
Phương pháp giải:
Xét hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\,\,\,\,\,\,\,\,\,\,(1)\\a'x + b'y = c'\,\,\,(2)\end{array} \right.\) có \(d\) là đường thẳng biểu diễn tập nghiệm của phương trình \(\left( 1 \right)\) và \(d'\) là đường thẳng biểu diễn tập nghiệm của phương trình \(\left( 2 \right)\), khi đó ta vẽ hai đường thẳng \(d\) và \(d'\) trên cùng hệ trục tọa độ để xác định số giao điểm của \(d\) và \(d'\) .
Từ đó suy ra số nghiệm của hệ đã cho.
Lời giải chi tiết:
Vẽ các đường thẳng \(2x + y = 4; - x + y = 1\) trong cùng một hệ tọa độ (h.8)
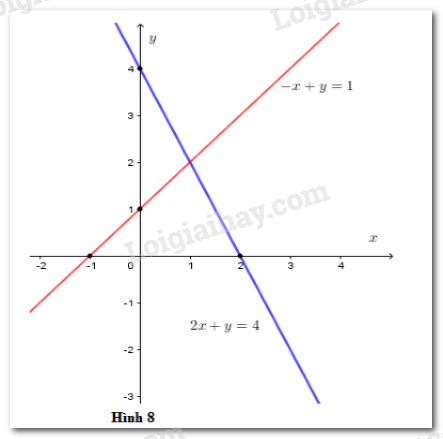
Ta thấy hai đường thẳng này cắt nhau tại một điểm.
Vậy hệ phương trình đã cho có nghiệm duy nhất.
soanvan.me
