Cho hai phương trình 2x + y = 4 và 3x + 2y = 5
LG a
Tìm nghiệm tổng quát của mỗi phương trình trên.
Phương pháp giải:
Sử dụng cách tìm nghiệm của phương trình bậc nhất hai ẩn \(ax + by = 0\,\left( {a,b \ne 0} \right)\) để tìm nghiệm tổng quát của mỗi phương trình đã cho.
Lời giải chi tiết:
Ta có \(2x + y = 4 \Leftrightarrow y = - 2x + 4\)
Vậy nghiệm tổng quát của phương trình thứ nhất là \(\left( {x; - 2x + 4} \right)\) với \(x \in \mathbb{R}.\)
Tương tự, \(3x + 2y = 5 \Leftrightarrow y = \dfrac{{ - 3}}{2}x + \dfrac{5}{2}\)
Vậy nghiệm tổng quát của phương trình thứ hai là \(\left( {x; - \dfrac{3}{2}x + \dfrac{5}{2}} \right)\) với \(x \in \mathbb{R}.\)
LG b
Vẽ các đường thẳng biểu diễn tập nghiệm của hai phương trình trong cùng một hệ trục tọa độ rồi xác định nghiệm chung của chúng.
Phương pháp giải:
Xác định tọa độ các điểm mà đường thẳng đi qua.
Vẽ các đường thẳng trên cùng hệ trục tọa độ để xác định nghiệm chung.
Lời giải chi tiết:
Đường thẳng \(2x + y = 4\) đi qua các điểm có tọa độ \(\left( {2;0} \right);\left( {1;2} \right)\)
Đường thẳng \(3x + 2y = 5\) đi qua các điểm có tọa độ \(\left( {1;1} \right);\left( { - 1;4} \right)\)
Vẽ hai đường thẳng trong cùng hệ tọa độ (h.9)
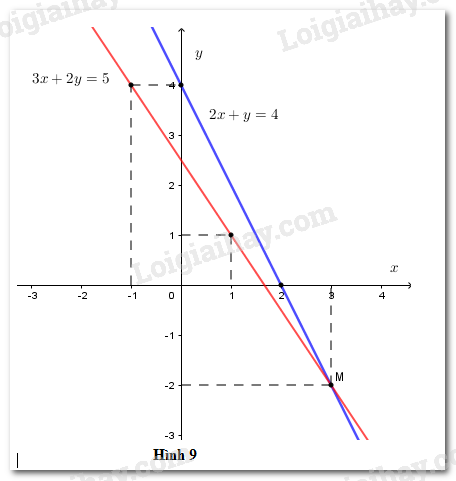
Hai đường thẳng cắt nhau tại \(M\left( {3; - 2} \right)\)
Thử lại, ta thấy \(\left( {3; - 2} \right)\) nghiệm đúng phương trình \(2x + y = 4\) (vì \(2.3 + \left( { - 2} \right) = 4\)) và phương trình \(3x + 2y = 5\) (vì \(3.3 + 2\left( { - 2} \right) = 5\)).
Vậy \(\left( {3; - 2} \right)\) là nghiệm chung của hai phương trình đã cho.
Chú ý:
Nói chung, việc xác định tọa độ của \(M\) chỉ cho kết quả gần đúng. Do đó, để chắc chắn cặp số tìm được (tọa độ của điểm \(M\)) là nghiệm của phương trình thì ta phải thử trực tiếp vào phương trình.
soanvan.me
