Đề bài
Cho hình lập phương \(ABCD.A'B'C'D'\). Chứng minh rằng:
a) Mặt phẳng \((AB'C'D)\) vuông góc với mặt phẳng \((BCD'A')\);
b) Đường thẳng \(AC'\) vuông góc với mặt phẳng \((A'BD)\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
a) Chứng minh \(AB' \bot \left( {BCD'A'} \right)\)
Sử dụng lý thuyết: Nếu một đường thẳng vuông góc với một mặt phẳng thì mọi mặt phẳng chứa nó đều vuông góc với mặt phẳng đã cho.
b) Chứng minh \(AC' \bot BD;\,\,AC' \bot A'D\)
Sử dụng lý thuyết: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó.
Lời giải chi tiết
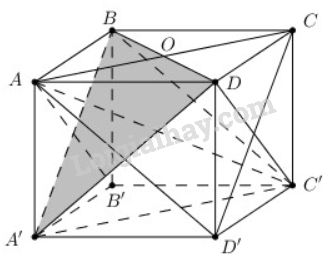
a)
\(\left\{ \begin{array}{l}
BC \bot AB\\
BC \bot BB'
\end{array} \right. \Rightarrow BC \bot \left( {ABB'A'} \right)\)
\( \Rightarrow BC ⊥ AB'\);
\( \left\{ \begin{array}{l}
AB' \bot BC\\
AB' \bot BA'\\
BC \cap BA' = B\\
BC,BA' \subset \left( {BCD'A'} \right)
\end{array} \right. \) \(\Rightarrow AB' \bot \left( {BCD'A'} \right)\)
Ta có \(AB' ⊂ (AB'C'D) \Rightarrow (AB'C'D) ⊥ (BCD'A')\)
b) +) \(AA'\bot(ABCD) \Rightarrow AA'\bot BD\)
Mà \(BD\bot AC\Rightarrow BD\bot (ACC'A')\)
\(AC'\subset(ACC'A')\) nên suy ra \(BD\bot AC'\) (1)
+) \(AB\bot (ADD'A')\Rightarrow AB\bot A'D \)
Mà \(AD'\bot A'D\Rightarrow A'D\bot (ABC'D')\)
Ta có \(AC'\subset (ABC'D')\Rightarrow A'D\bot AC'\) (2)
Từ (1) và (2) suy ra: \(AC' ⊥ (A'BD)\).
soanvan.me
